✖

Absolutní hodnota

Absolutní hodnota z čísla je vždy číslo nezáporné, tedy větší nebo rovno nule. Pokud máme vypočítat absolutní hodnotu z čísla kladného, bude to vždy to samé číslo. Budeme-li ovšem chtít zjistit absolutní hodnotu ze záporného čísla, bude to číslo opačné (tedy z x, kde x < 0 bude absolutní hodnota −x. Absolutní hodnota se značí dvěma svislými čárami: |x|.

Základní vlastnosti

Ač se zdá, že počítání s absolutními hodnotami bude hračka, spíše opak je pravdou, většinou dokáží pěkně znepříjemnit jinak lehkou funkci. Viz například lineární rovnice s absolutní hodnotou. Uveďme ještě několik příkladů:

$$\begin{eqnarray} |5| &=& 5\\ |0| &=& 0\\ |-12| &=& 12\\ |3{,}14| &=& 3{,}14\\ |-2{,}71| &=& 2{,}71 \end{eqnarray}$$

Absolutní hodnota má tyto vlastnosti, pro hodnoty a, b, c z množiny reálných čísel:

  1. |x| ≥ 0
  • |a · b| = |a| · |b|
  • |a + b| ≤ |a| + |b|
  • |a| ≤ b ⇔ −b ≤ a ≤ b

Zvlášť se počítá absolutní hodnota u komplexních čísel.

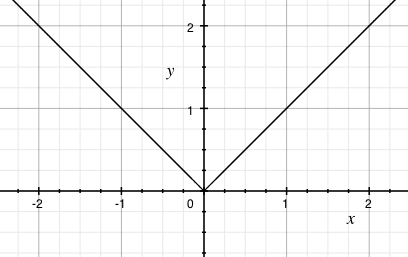
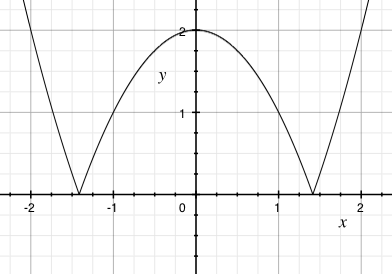
Grafy

Grafy funkcí s absolutní hodnotou se vyznačují tím, že vytvářejí křivky do „špičky“. V tomto bodě pak funkce není derivovatelná.

Graf funkce f(x)=|x| Graf funkce f(x)=|x^2-2|

Kalkulačka

Pro výpočet absolutní hodnoty můžete použít kalkulačku.