Goniometrický tvar komplexního čísla

Ne vždy se vyplatí mít komplexní číslo v algebraickém tvaru a proto se zavádí ještě goniometrický tvar komplexního čísla.

Jak lze vyjádřit bod v rovině?

Víme, že v geometrickém vyjádření představuje komplexní číslo z = x + yi bod v Gaussově rovině. Tento bod má souřadnice [x, y]. Jakým dalším způsobem můžeme ještě definovat daný bod z krom vypsání souřadnic [x, y]?

Můžeme vypočítat, jaký úhel svírá spojnice bodu z a počátku s osou x (resp. její kladnou poloosou). Tím budeme vědět, kterým směrem leží bod z směrem od počátku. Abychom zjistili, kde leží přesně, potřebujeme ještě znát vzdálenost od počátku. S těmito dvěma údaji už jsme schopni přesně definovat bod z v Gaussově rovině.

Goniometrický tvar

Následující obrázek shrnuje, co vše potřebujeme znát, abychom mohli vyjádřit komplexní číslo v goniometrického tvaru:

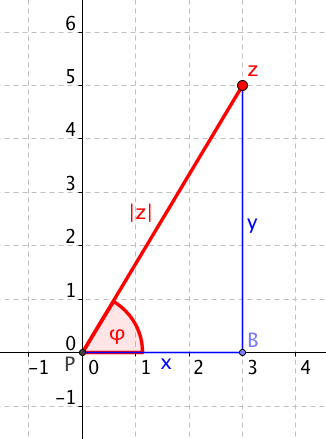
Jak je vidět, potřebujeme znát délku spojnice od bodu z k počátku, což je rovno absolutní hodnotě čísla z — to už umíme spočítat. Dále potřebujeme znát úhel $\varphi$. Goniometrický tvar komplexního čísla pak vypadá takto:

$$z=|z|(\cos\varphi+i\sin\varphi)$$

Jak zjistíme úhel $\varphi$? Využijeme k tomu goniometrické funkce. Máme zde pravoúhlý trojúhelník a známe délku přepony, to je absolutní hodnota čísla z. V goniometrickém tvaru máme jak sinus, tak cosinus, takže musíme úhel $\varphi$ vyjádřit pomocí obou funkcí. Přitom ale, z vlastností goniometrických funkcí, platí, že:

$$\begin{eqnarray} \sin\varphi&=&\frac{y}{|z|}\\ \cos\varphi&=&\frac{x}{|z|} \end{eqnarray}$$

Z těchto vzorců můžeme odvodit samotný úhel $\varphi$. Odvodit úhel je nutné, protože goniometrický tvar zapisujeme včetně sinu a kosinu.

Příklad

Převeďte komplexní číslo v algebraické tvaru do goniometrického tvaru: $z=\sqrt{3}+i$. Jako první vypočítáme absolutní hodnotu čísla z, což se rovná:

$$|z|=\sqrt{3+1}=2$$

Nyní tak platí:

$$\begin{eqnarray} \sin\varphi&=&\frac{1}{2}\\ \cos\varphi&=&\frac{\sqrt{3}}{2} \end{eqnarray}$$

V tuto chvíli můžeme buď použít kalkulačku a spočítat arcus sinus a arcus cosinus, nebo můžeme využít tabulky základních goniometrických vzorců. Obě hodnoty, které nám vyšly, jsou tabulkové, takže pro tentokrát kalkulačku nepoužijeme.

Pokud platí, že $\sin\varphi=\frac12$, pak je úhel $\varphi$ roven buď π/6 nebo 5π/6. Pokud platí, že $\cos\varphi=\frac{\sqrt{3}}{2}$, pak je úhel $\varphi$ roven buď úhlu π/6 nebo 11π/6. Průnikem těchto možností je úhel π/6, použitím tohoto úhlu dostaneme hodnoty, které jsme si zapsali v předchozí rovnici.

Násobení a dělení

Komplexní čísla v goniometrickém tvaru můžeme samozřejmě násobit či dělit. Za pomocí součtových goniometrických vzorců lze odvodit vzorce pro součin a podíl dvou komplexních čísel. Mějme dvě komplexní čísla z₁ a z₂:

$$\begin{eqnarray} z_1&=&|z_1|(\cos\varphi_1+i\sin\varphi_1)\\ z_2&=&|z_2|(\cos\varphi_2+i\sin\varphi_2) \end{eqnarray}$$

Samotné vzorce vypadají takto:

$$\begin{eqnarray} z_1\cdot z_2&=&|z_1|\cdot|z_2|\left[\cos(\varphi_1+\varphi_2)+i\sin(\varphi_1+\varphi_2)\right]\\ \frac{z_1}{z_2}&=&\frac{|z_1|}{|z_2|}\left[\cos(\varphi_1-\varphi_2)+i\sin(\varphi_1-\varphi_2)\right] \end{eqnarray}$$

Další zdroje

• Diplomová práce na cuni.cz
• maths.cz