Grafické znázornění komplexních čísel

Komplexní čísla můžeme zobrazovat i v klasické kartézské soustavě souřadnic. Rovina, kde komplexní čísla zobrazujeme, se nazývá rovina komplexních čísel nebo také Gaussova rovina.

Zobrazení v Gaussově rovině

Každé komplexní číslo z = x + yi je zobrazeno v rovině bodem o souřadnicích [x, y]. Osa x se v Gaussově rovině nazývá osa reálných čísel a osa y se nazývá osa imaginárních čísel. Takže mějme dvě komplexní čísla, z₁ = 2 + 5i a z₂ = 4 − 3i. V Gaussově rovině bychom je zobrazili takto:

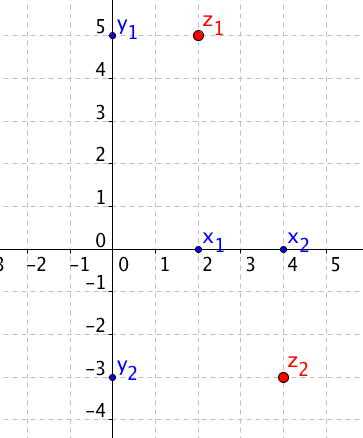
Opačné a komplexně sdružené číslo

Na Gaussově rovině můžeme snadno zanést opačná a komplexně sdružená čísla. Mějme komplexní číslo z = 3 + 5i. Opačné číslo o číslu z, které má tvar −3 − 5i, je souměrné s počátkem Gaussovy roviny:

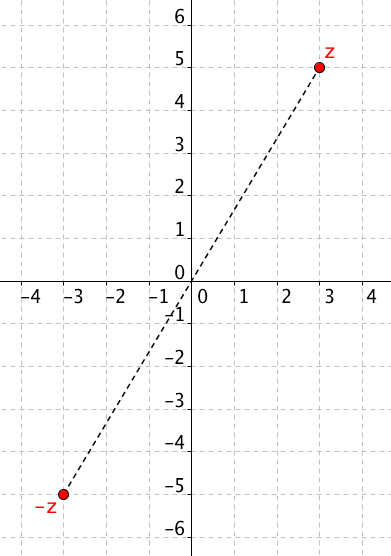
U komplexně sdruženého čísla se mění znaménko u imaginární části, takže komplexně sdružené číslo bude s původním číslem osově souměrně podle reálné osy (osy x). Viz obrázek ($z^\prime$ značí komplexně sdružené číslo):

Absolutní hodnota

V oboru reálných čísel představuje absolutní hodnota kladnou verzi daného čísla. V komplexních číslech počítáme absolutní hodnotu trochu složitěji. Absolutní hodnota komplexního čísla totiž představuje vzdálenost bodu v Gaussově rovině od jeho počátku.

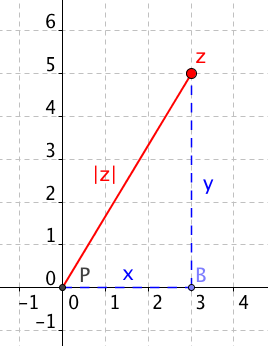
Vzdálenost od počátku můžeme vypočítat pomocí Pythagorovy věty, která nám říká, že |z|² = x² + y², kde x a y je reálná a imaginární část komplexního čísla. Absolutní hodnotu čísla z = x + yi pak už jen získáme odmocněním:

$$|z|=\sqrt{x^2+y^2}$$