Obecná rovnice přímky

Obecnou rovnici přímky získáme z parametrické rovnice přímky tak, že odstraníme parametr t.

Motivace

Vzpomínáte si na lineární funkci? Ta má jako svůj graf právě přímku. Základní tvar lineární funkce je přitom y = ax + b. Podívejme se na přímku p, která prochází body A[0,3], B[2,7]:

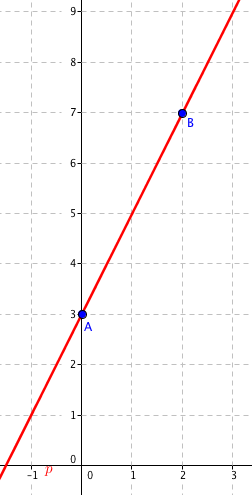
Určíme lineární funkci, která má za graf právě tuto přímku p. Tato lineární funkce má tvar y = ax + b, přitom to, že přímka prochází bodem A[0,3] nám říká, že v bodě x₁ = 0 má funkce funkční hodnotu y₁ = 3. Musí tak platit rovnice a · 0 + b = 3. Protože přímka prochází o bodem B[2,7], má funkce v bodě x₂ = 2 funkční hodnotu y₂ = 7 musí zároveň platit rovnice a · 2 + b = 7. My hledáme koeficienty a, b. Vzniká nám soustava rovnic:

$$\begin{eqnarray} a \cdot 0 + b &=& 3\\ a \cdot 2 + b &=& 7 \end{eqnarray}$$

Z první rovnice a · 0 + b = 3 můžeme snadno získat koeficient b, který je tak roven b = 3. Tento výsledek dosadíme do druhé rovnice, tedy do rovnice a · 2 + b = 7 dosadíme za b číslo tři:

$$\begin{eqnarray} a \cdot 2 + b &=& 7\\ a \cdot 2 + 3 &=& 7\\ a \cdot 2 &=& 4\\ a &=& 2 \end{eqnarray}$$

A máme oba koeficienty: a = 2, b = 3. Funkce, která popisuje předchozí přímku, má tvar y = 2x + 3. Když za x dosadíme x = 1, dostáváme y = 2 + 3 = 5, což souhlasí s grafem přímky. Tvar y = 2x + 3 můžeme ještě přepsat tak, aby na pravé straně byla nula, tj. přičteme k rovnici −(2x + 3). Tím získáme rovnici:

$$ y-2x-3=0 $$

Tato rovnice se nazývá obecná rovnice přímky.

Definice obecné rovnice přímky

Předchozí postup je mírně složitý a navíc není použitelný v případě, kdy je přímka rovnoběžná s osou y, tj. když je vertikální, protože taková přímka nepopisuje žádnou funkci. Obecnou rovnici přímky proto zavedeme ještě jiným způsobem. Řekneme, že každá lineární rovnice tvaru

$$ ax + by + c = 0, $$

kde a,b,c∈ ℝ a alespoň jedno z čísel a,b ≠ 0, je rovnice přímky v rovině. Přitom každá přímka v rovině lze vyjádřit v tomto tvaru. Tuto rovnici pak nazýváme obecnou rovnicí přímky. Můžeme ji jednoduše zjistit z parametrického tvaru přímky. Máme-li přímku popsanou parametrickou rovnicí

$$\begin{eqnarray} x &=& a_1 + t\cdot u_1\\ y &=& a_2 + t\cdot u_2,\\ \end{eqnarray}$$

zjistíme obecnou rovnici tak, že z parametrické rovnice odstraníme parametr t. Příklad: držme se předchozí přímky danou body A[0,3], B[2,7]. Zjistíme směrový vektor $\vec{\mathbf{u}}$ z orientované úsečky $\vec{AB}$.

$$ \vec{\mathbf{u}}=(u_1, u_2)=B-A=[2{,}7]-[0{,}3]=[2{,}4] $$

Můžeme si znovu prohlédnout přímku p se směrovým vektorem $\vec{\mathbf{u}}$:

Vyjádříme parametrickou rovnici vzhledem k bodu A a vektoru $\vec{\mathbf{u}}$:

$$\begin{eqnarray} x &=& 0 + t\cdot 2\\ y &=& 3 + t\cdot 4\\ \end{eqnarray}$$

Abychom dostali obecnou rovnici, musíme tyto dvě rovnice sečíst tak, abychom vyrušili parametr t. Jako první tak vynásobíme první rovnici −2, druhou nezměníme:

$$\begin{eqnarray} -2x &=& 0 - t\cdot 4\\ y &=& 3 + t\cdot 4\\ \end{eqnarray}$$

A teď obě rovnici sečteme, čímž získáme jednu rovnici:

$$\begin{eqnarray} y-2x &=&3 +t \cdot 4 - t \cdot 4\\ y-2x &=&3\\ y-2x-3 &=&0 \end{eqnarray}$$

Toto je výsledná obecná rovnice přímky p. Vidíme, že jsme získali úplně stejnou rovnici jako v předchozím postupu.

K čemu je obecná rovnice přímky

Obecná rovnice nám určuje všechny body, které tvoří přímku. Pokud do obecné rovnice ve tvaru ax + by + c = 0 dosadíme za neznámé x,y takové reálná čísla, aby měla rovnice smysl, pak [x,y] je bodem této přímky. Vraťme se k předchozí přímce popsanou obecnou rovnicí y − 2x − 3 = 0. Pokud za x,y dosadíme hodnoty x = 1, y = 5, získáme rovnici:

$$\begin{eqnarray} 5-2\cdot1-3&=&0\\ 5-2-3&=&0\\ 0&=&0 \end{eqnarray}$$

To znamená, že bod [1,5] leží na přímce. Když zkusíme dosadit x = 2, y = 3, získáme rovnici:

$$\begin{eqnarray} 3-2\cdot2-3&=^?&0\\ 3-4-3&=^?&0\\ -4&\ne&0 \end{eqnarray}$$

Rovnice nemá smysl, bod [2,3] neleží na přímce p. Můžeme si to i zkontrolovat na obrázku:

Vertikální přímka

Už jsme nakousli, že obecnou rovnici vertikální přímky p bychom nemohli získat pomocí postupu popsaného v první kapitole, protože vertikální přímka nepopisuje žádnou funkci. Nicméně i taková přímka má svou obecnou rovnici, kterou získáme postupem uvedeným v předchozí kapitole.

Ukážeme si to na přímce, která prochází body A[4,2], B[4,8]. Směrový vektor $\vec{\mathbf{u}}$ má tvar:

$$ \vec{\mathbf{u}}=(u_1,u_2)=B-A=[4{,}8]-[4{,}2]=[0{,}6] $$

Obrázek:

Parametrická rovnice vzhledem k bodu A a směrovému vektoru $\vec{\mathbf{u}}$ by vypadala takto:

$$\begin{eqnarray} x &=& 4 + t\cdot 0\\ y &=& 2 + t\cdot 6\\ \end{eqnarray}$$

Nyní bychom měli odstranit parametr t. Nicméně první rovnice nám už ušetřila práci, v první rovnici žádný parametr t není, respektive je vždy nulový, takže můžeme celou tuto rovnici použít jako obecnou rovnici přímky p. Přímka p tak má obecnou rovnici

$$ x-4=0 $$

Tedy koeficienty a,b,c v rovnici ax + by + c = 0 se rovnají a = 1, b = 0, c = −4.

Horizontální přímka

Ukážeme si ještě jeden příklad, s horizontální přímkou, která prochází body A[2,1], B[5,1]. Směrový vektor $\vec{\mathbf{u}}$ bude roven:

$$ \vec{\mathbf{u}}=(u_1,u_2)=B-A=[5{,}1]-[2{,}1]=[3{,}0] $$

Obrázek:

Parametrická rovnice přímky vzhledem k bodu A by vypadala takto:

$$\begin{eqnarray} x &=& 2 + t\cdot 3\\ y &=& 1 + t\cdot 0\\ \end{eqnarray}$$

Opět vidíme, že nemusíme eliminovat parametr t, protože ve druhé rovnici je nulový. Můžeme tak použít přímo druhou rovnici jako obecnou rovnici přímky p:

$$ y-1=0 $$

Odkazy a zdroje

• J. Polák: Přehled středoškolské matematiky