Rozptyl
Rozptyl nám udává, jak moc jsou hodnoty v našem statistickém soubory rozptýleny. Rozptylu se někdy též říká variance.
Co je to rozptyl
Podívejte se na následující tabulku, která zachycuje výsledné známky na vysvědčení deseti vybraných žáků osmé bé. Budou nás zajímat dva předměty, matematika a dějepis.
| Jméno | Matematika | Dějepis |
|---|---|---|
| Tomáš | 2 | 4 |
| Martin | 1 | 1 |
| Jiří | 2 | 1 |
| Miroslav | 2 | 1 |
| Jana | 2 | 3 |
| Lenka | 1 | 4 |
| Ondřej | 2 | 5 |
| Lukáš | 2 | 1 |
| Petra | 2 | 2 |
| Jan | 3 | 4 |
Vidíme, že většina žáků má z matematiky dvojku, občas má někdo jedničku nebo trojku. Zatímco ve sloupci s dějepisem máme celkem chaos — známky jsou rozptýlené od jedničku po pětku a žádná známka ani výrazně nepřevažuje. Známky z dějepisu jsou tak více rozptýlené než známky z matematiky.
Když si spočítáme průměrnou známku z matematiky, vyjde nám 1,9. Vidíme, že většina prvků se pohybuje poměrně blízko této hodnoty. Naopak u dějepisu nám vychází průměr 2,6 a většina známek se nepohybuje blízko této hodnoty.
Jak bychom číselně vyjádřili tento rozptyl?
Jak spočítat rozptyl
Předchozí graf si převedeme do trochu jiné podoby a zobrazíme pouze známky z dějepisu.
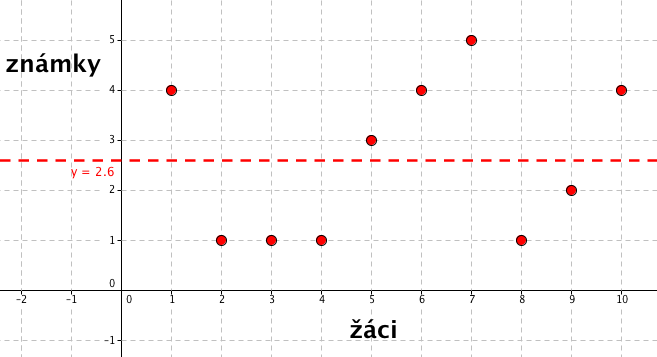
Na ose x máme opět žáky (tentokrát bez jmen, takže předpokládejme, že 1 = Tomáš, 2 = Martin atp.). Na ose y máme výsledné známky. Přímka y = 2,6 představuje průměrnou hodnotu.
Rozptyl pak spočítáme jako průměr druhých mocnin vzdáleností od průměru. To zní tajemně, ale je to jednoduché. Druhou mocninu x si můžeme představit jako obsah čtverce o délce strany x. Vytvoříme tak v našem grafu čtverce, které budou mít délku strany rovnou vzdáleností hodnoty od průměru:
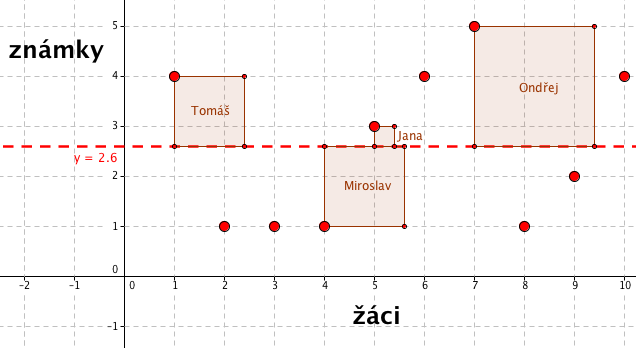
V grafu jsou znázorněny čtyři takové čtverce, všechny by se tam nevešly. Vidíme, že Jana je celkem blízko průměru, proto je její čtverec malý. Zatímco Ondřej je daleko od průměru, proto je čtverec velký. Pokud bychom sestrojili všechny čtverce a spočítali bychom průměrný obsah těchto čtverců, tak bychom získali rozptyl.
Máme-li soubor hodnot X = [x1, …, xN], kde $\overline{x}$ je průměrná hodnota, pak rozptyl, označme ho $\mbox{Var}$, vypočítáme takto:
$$ \mbox{Var}(X) = \frac1N \left((x_1-\overline{x})^2 + (x_2-\overline{x})^2 + … + (x_N-\overline{x})^2 \right) $$
Případně pomocí sumy takto:
$$ \mbox{Var}(X) = \frac1N\sum_{i=1}^N (x_i-\overline{x})^2 $$
Proč zrovna $(x_1-\overline{x})^2$? Samotný výraz $x_1-\overline{x}$ by nám vrátil vzdálenost bodu x1 od průměru. Přesněji bychom měli napsat $|x_1-\overline{x}|$ (absolutní hodnota), kdyby byla hodnota x1 menší než hodnota průměru. Protože chceme znát obsah čtverce, umocníme tuto hodnotu na druhou.
Rozptyl našeho souboru dat by tak byl:
$$ \begin{align*} Var(\mbox{Dejepis}) = \frac{1}{10}((4-2{,}6)^2+(1-2{,}6)^2+(1-2{,}6)^2+\\(1-2{,}6)^2+(3-2{,}6)^2+(4-2{,}6)^2+\\(5-2{,}6)^2+(1-2{,}6)^2+(2-2{,}6)^2+\\(4-2{,}6)^2)=\frac{1}{10}\cdot 22{,}4 = 2{,}24 \end{align*} $$
Rozptyl (variance) je 2,26. Rozptyl hodnot s výsledky z matematiky by vypadal takto:
$$ \begin{align*} Var(\mbox{Matematika}) = \frac{1}{10}((2-1{,}9)^2+(1-1{,}9)^2+(2-1{,}9)^2+\\(2-1{,}9)^2+(2-1{,}9)^2+(1-1{,}9)^2+\\(2-1{,}9)^2+(2-1{,}9)^2+(2-1{,}9)^2+\\(3-1{,}9)^2)=\frac{1}{10}\cdot2{,}9 = 0{,}29 \end{align*} $$
Rozptyl (variance) je 0,29. Vidíme, že rozptyl u tohoto souboru je, dle očekávání, mnohem menší.
Jak vypočítat rozptyl v Excelu
V českém i anglickém Excelu k tomu slouží funkce var, respektive nějaká její varianta. Například var.p za parametr dosadíme výběr buněk.

