Sudá a lichá funkce

U funkcí můžeme určovat jejich paritu, tedy můžeme určit, jestli je funkce sudá nebo lichá. V krajním případě může být sudá i lichá zároveň, ale většinou nebývá ani sudá ani lichá.

Sudost

Funkce je sudá, pokud splňuje jednoduché pravidlo — když do funkce vložíte prvek x a poté inverzní prvek −x, pak musí funkce vrátit stejnou výslednou hodnotu. Typickou sudou funkcí je funkce f(x) = x². Pokud ji zavoláte s argumenty 6 a −6, získáte: f(6) = 36 a f(−6) = 36. Argument se lišil jen ve znaménku, výsledek je tak stejný.

Formální definice by mohla vypadat takto. Pokud je funkce f sudá, pak musí splňovat

$$\forall x\in D(f): f(x)=f(-x)$$

Pro všechny x z definičního oboru funkce musí platit, že i když funkci zavoláme s inverzním argumentem, tj. −x, tak se funkční hodnoty musí rovnat.

Jak se projeví sudá funkce v grafu? Pokud do funkce vložíme x a −x, pak získáme stejné y. Takže když se nad tím zamyslíme: x a −x je na x-ové ose stejně vzdáleno od počátku a mají stejnou y-ovou souřadnici. Znamená to, že graf sudé funkce je souměrný podle y-ové osy. Pro ilustraci graf funkce x²:

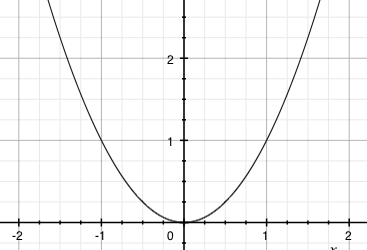
Z klasických funkcí jsou sudé funkce: kosinus, funkce ve tvaru f(x) = x^a, kde a je sudé číslo. Z původně liché funkce nám sudou funkci udělá absolutní hodnota, například f(x) = |x|, f(x) = |x³|, f(x) = |1/x|.

Lichá funkce

Funkce lichá musí splňovat podobná pravidla jako sudá funkce. Takže funkce f je lichá, pokud splňuje toto pravidlo:

$$\forall x\in D(f): f(-x)=-f(x)$$

V praxi to znamená, že pokud liché funkci náleží bod [a, b], pak jí musí náležet i bod s inverzními souřadnicemi, tedy [−a, −b]. Příkladem liché funkce je funkce f(x) = x³. Pokud za x dosadíme dvojku, dostáváme:

$$f(-x)=f(-2)=(-2)^3=-8$$

Ve druhém výrazu bychom dostali

$$-f(x)=-f(2)=-(2^3)=-8$$

Jak se to projeví v grafu? Pokud má funkci náležet bod [a, b] a zároveň [−a, −b]? Když si to nakreslíte, zjistíte, že takový graf bude souměrný s počátkem souřadnicového systému, tj. bodu [0, 0]. Graf funkce f(x) = x³ je zobrazen na následujícím obrázku.

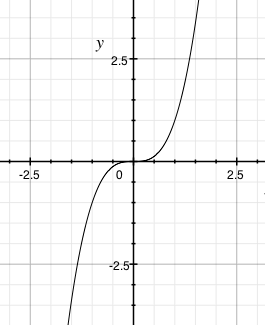
Z klasických funkcí jsou liché funkce: f(x) = x^a, kde a je liché, f(x) = ax, kde a je libovolné reálné číslo (jedná se tedy o lineární funkci bez absolutního členu). Dále ještě f(x) = a/x nebo sinus.

Ověření sudosti

Jak ověříme, jestli je funkce sudá? Musíme podle definice. Takže například známá funkce f(x) = x². Ověříme podle definice. Ta nám říká, že f(x) = f(−x). Pokud je funkce sudá, musí splňovat:

$$x^2=(-x)^2$$

Minus x na druhou můžeme podle pravidel počítání s mocninami rozepsat takto:

$$x^2=(-1)^2\cdot x^2$$

Minus jedna na druhou je jedna, takže dostáváme zpátky jen x².

$$x^2=1\cdot x^2$$

Je následující funkce sudá?

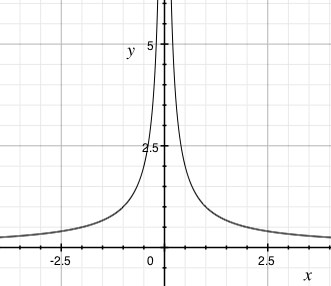
$$f(x)=\left|\frac{1}{x}\right|$$

Dosadíme do definice:

$$\left|\frac{1}{x}\right|=\left|\frac{1}{-x}\right|$$

Tyto zlomky můžeme přeskládat tak, že místo toho, abychom absolutní hodnotu měli na celý zlomek, přesuneme ji do čitatele a jmenovatele.

$$\frac{|1|}{|x|}=\frac{|1|}{|-x|}$$

Upravíme jmenovatel druhého zlomku, protože jistě platí |x| = |−x|, z definice absolutní hodnoty.

$$\frac{|1|}{|x|}=\frac{|1|}{|x|}$$

Teď už dostáváme rovnost.

Ověření lichosti

Jak ověříme, jestli je funkce lichá? Musíme opět podle definice. Ta říká, že funkce f je lichá, pokud

$$f(-x)=-f(x)$$

Začněme s funkcí f(x) = x³. Dosadíme do definice:

$$(-x)^3=-x^3$$

Levou stranu si můžeme rozepsat stejně jako v minulém příkladě:

$$(-1)^3\cdot x^3=-x^3$$

Minus jedna na třetí je minus jedna:

$$-1\cdot x^3=-x^3$$

Takže máme rovnost:

$$-x^3=-x^3$$

Funkce je lichá.

Je daná funkce lichá?

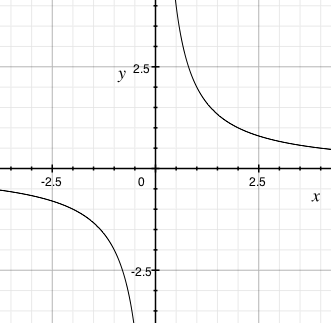
$$f(x)=\frac{2}{x}$$

Dosadíme do definice:

$$\frac{2}{-x}=-\frac{2}{x}$$

Není tady moc co upravovat, minusko v prvním zlomku jednoduše vytkneme před celý zlomek, takže dostaneme rovnost:

$$-\frac{2}{x}=-\frac{2}{x}$$

Funkce je lichá.

Ani sudá, ani lichá

Funkce nemusí být ani sudá, ani lichá. Takových funkcí je asi většina. Příkladem budiž lineární funkce f(x) = x + 1. zkusíme dosadit do definice sudosti:

$$x+1=-x+1$$

Osamostatníme x:

$$\begin{eqnarray} x+1&=&-x+1\\ 2x+1&=&1\\ 2x&=&0 \end{eqnarray}$$

rovnost neplatí pro všechna x, ale jen pro některá, takže funkce není sudá. Teď lichost:

$$\begin{eqnarray} -x+1&=&-(x+1)\\ -x+1&=&-x-1\\ 0x&=&-2 \end{eqnarray}$$

Tato rovnice dokonce nemá řešení nikdy, proto funkce není lichá.

Sudá i lichá

Existuje funkce, která by byla sudá i lichá zároveň? Existuje graf funkce, který by byl souměrný podle y-ové osy a zároveň podle počátku? Odpovědí je, že ano Existuje právě jedna funkce, která je sudá i lichá zároveň a je to konstantní funkce f(x) = 0. Graf funkce přesně kopíruje osu x.

Poznámka: ve skutečnosti existuje nekonečně mnoho takových funkcí, protože si můžeme definovat funkci g(x), která bude mít stejný předpis, jen bude definována na jiném definičním oboru. Například můžeme mít funkci g(x) = 0, která bude mít definiční obor pouze přirozená čísla. Tato funkce se liší od funkce f(x), která je definována nad reálnými čísly. Nicméně předpis bude vždy stejný.

Složené funkce

Zajímavá situace nastane, pokud máme dvě funkce, které jsou liché nebo sudé a pokusíme se je sečíst, vynásobit apod. Například výsledkem sčítání dvou sudých funkcí vyjde opět funkce sudá. Pravidel a kombinací je spousta, můžete se podívat na přehlednou tabulku u kolegy (kapitola složené funkce).