Exponenciální funkce

Exponenciální funkce je taková funkce, která má neznámou na místě exponentu.

Definice

Exponenciální funkce f má tvar

$$f(x)=a^x,\quad a\in\mathbb{R},\quad a>0,\quad a\ne1$$

Symbol a je libovolné číslo, není to žádný složitější výraz; nazývá se základ. Výraz x se nazývá exponent. Základem tak může být například celé číslo 3, racionální číslo $\frac12$ nebo konstanta π.

Proč klademe podmínky na základ a? Pokud by bylo a rovno jedné, dostali bychom konstantní funkci, protože „jedna na cokoliv“ je vždy jedna. Platí, že 1² = 1, 1⁹ = 1, 1⁶⁶⁶ = 1. A protože konstantní funkci mezi exponenciální nezařazujeme, musí být a různé od jedničky, proto a≠1. Ze stejného důvodu musí platit a≠0.

A proč musí platit a>0? Protože mocnina samotná je definovaná jen pro kladná čísla. Například pokud bychom za x zvolili jednu polovinu, tak pokud bychom počítali $a^{\frac12}$, je to totéž, jako bychom počítali odmocninu z čísla a. Přitom platí, že odmocnit můžeme pouze nezáporné číslo.

Pokud splníme předchozí podmínky, má exponenciální funkce f(x) = a^x definiční obor reálná čísla.

Kvadratická vs. exponenciální funkce

Exponenciální funkci si můžete snadno poplést s kvadratickou funkcí. Platí, že kvadratická funkce má neznámou jako základ a jako exponent má číslo, zatímco exponenciální funkce má jako základ číslo a v exponentu má neznámou. Takže kvadratická funkce jsou například tyto funkce: x², x² + 4 nebo x² − x + 1. Exponenciální funkce jsou funkce: 2^x, 4^x nebo π^x.

Důležité exponenciální funkce

Významnou exponenciální funkcí je „přirozená exponenciální funkce“. Je to funkce, která má základ konstantu e, tj. Eulerovo číslo. Eulerovo číslo je iracionální číslo, tj. číslo s nekonečným desetinným rozvojem, nelze ho přesně vyčíslit. Jeho přibližná hodnota je e = 2,718 281 828… Tato funkce se často značí jako exp.

Další důležitou exponenciální funkcí je „dekadická exponenciální funkce“, která má základ rovný deseti: a = 10.

Podoba funkce v závislosti na hodnotě a

Funkce má dvě základní podoby, liší se podle toho, jaká je hodnota základu. Rozlišujeme totiž dva intervaly: (0,1) a (1, ∞). Pokud je a z prvního intervalu, tj. je menší než jedna, pak je totiž funkce klesající. Pokud je z druhého intervalu, pak je rostoucí. Má to samozřejmě logiku. Pro příklad si vezměme $a=\frac12$, tj. funkci $f(x)=\frac12^x$. Co se stane, pokud za x dosadíme postupně dvojku, trojku a čtyřku? Hodnota funkce bude postupně klesat, dostaneme totiž: $f(2)=\frac12^2 = \frac12 \cdot \frac12=\frac14$, dále $f(x)=\frac12^3= \frac12 \cdot \frac12 \cdot \frac12$, což je rovno $\frac18$. Pro f(4) dostaneme polovinu jedné osminy, tj. $\frac{1}{16}$. Dostáváme stále menší čísla, protože základ je menší než jedna. Pokud násobíme čísla, která jsou menší než jedna, dostaneme vždy číslo menší.

Naopak, pokud je a>1, pak bude výsledkem násobení číslo větší. Pokud máme exponenciální funkci f(x) = 3^x, dostáváme pro hodnoty dva, tři čtyři výsledky: f(2) = 3² = 3 · 3 = 9. Pro trojku: f(3) = 3³ = 3 · 3 · 3 = 27. Dále f(4) = 81. Funkce je tak rostoucí. Všimněte si, že i kdyby základ bylo jakékoliv jiné číslo, které je větší než jedna, tak funkce bude stále rostoucí.

Proto musíme rozlišovat i dva typy grafů v závislosti na hodnotě základu a.

Grafy exponenciálních funkcí

Z předchozí kapitoly víme, že graf musí mít dvě základní podoby v závislosti na hodnotě základu a. Jako první si ukážeme graf pro hodnoty a z intervalu (0, 1).

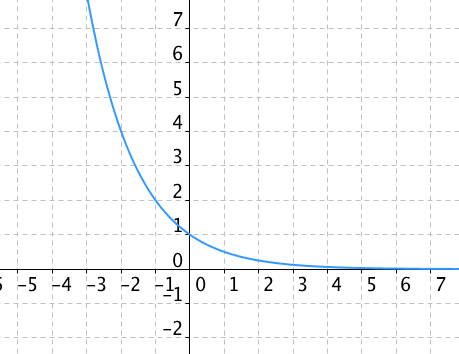
Vidíme, že funkce je klesající a prochází bodem [0, 1]. To není náhoda — z vlastností mocnin víme, že cokoliv na nultou je jedna. Tedy $\frac12^0=1, 5^0=1, 33^0=1$ apod. Proto i každá křivka exponenciální rovnice musí procházet tímto bodem. I ta křivka, která bude odpovídat exponenciální funkci při a>1, jako je vidět na následujícím obrázku:

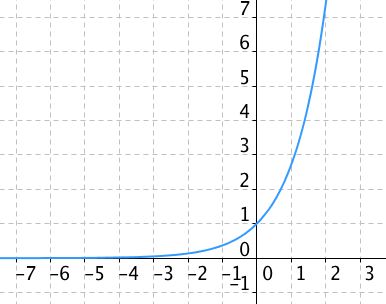
Vlastnosti exponenciálních funkcí

• Definiční obor je množina všech [reálných čísel](reálná čísla)
• Obor hodnot je interval (0, ∞)
• Je zdola omezená, a^x>0. Shora neomezená.
• Nemá maximum, ani minimum.

Monotonnost funkce pak záleží na hodnotě a. Pokud je a z intervalu (0, 1), pak je funkce klesající. Pokud je z intervalu (1, ∞), pak je rostoucí.

Exponenciální růst

Pojem „Exponenciální růst“ se používá poměrně často i v běžné mluvě. Obyčejně tím chce člověk říci, že něco stoupá strašně rychle. Klasickým případem může být dělení bakterií, jak to známe ze seriálu Byl jednou jeden život. Jednou za čas se tam objevil zlá bakterie, která se začala množit tak, že se vždy rozdvojila. Tento způsob množení můžeme popsat exponenciální funkcí f(x) = 2^x. Funkční hodnota nám bude udávat počet bakterií po x kolech dělení.

Příklad: na začátku (nulový počet rozdvojení, x = 0) máme jednu bakterii, tedy 2⁰ = 1. Po prvním kole množení máme 2¹ = 2, tj. dvě bakterie. To sedí, jedna bakterie se rozdvojí na dvě. Nyní se obě z těchto bakterií rozdvojí, tj. máme 2² = 4 čtyři bakterie. Opět se každá rozdvojí, takže po třetím kole už máme 2³ = 8 bakterií. A tak dále.

Toto množení, ač se to nezdá, je strašně rychlé. Kolik bakterií máme po desátém kole? 2¹⁰ = 1024. To už je hezké číslo. Po dvaceti kolech máme: 2²⁰ = 1 048 576. Po třiceti kolech se už dostáváme přes miliardu.

Tato rychlost je mnohem větší než v případě obyčejné kvadratické rovnice. Pokud bychom srovnali rychlost exponenciální funkce f(x) = 2^x a kvadratické funkce g(x) = x², exponenciální funkce jednoznačně zvítězí. Už známe hodnotu funkce f v bodě x = 20, přitom hodnota kvadratické funkce g v bodě x = 20 je rovna: g(20) = 20² = 400. To je mnohonásobně méně než 1 048 576.