Parametrická kvadratická rovnice

Parametrická kvadratická rovnice se od normální kvadratické rovnice liší tím, že obsahuje navíc parametr, často označovaný jako p nebo m. Naším úkolem je pak zjistit, jaké má kvadratická rovnice řešení v závislosti na tomto parametru p.

První příklad

Máme následující kvadratickou rovnici s parametrem p.

$$x^2+2px+9=0.$$

Jaká různá řešení má rovnice v závislosti na parametru p? Můžeme rozlišovat celkem tři případy — rovnice nemá řešení v oboru reálných čísel, rovnice má dvě stejná řešení a rovnice má dvě různá řešení. Tyto případy rozlišíme pomocí diskriminantu.

Parametr se chová jako konstanta, tj. pro předchozí kvadratickou rovnici platí, že a = 1, b = 2p a c = 9. Nyní vypočítáme diskriminant tak, jak jsme zvyklí:

$$D=b^2-4ac=4p^2-4\cdot1\cdot9=4p^2-36.$$

Takže diskriminant nám vyšel D = 4p² − 36. Nyní musíme zjistit, kdy je tento diskriminant kladný, záporný a nulový.

Začněme nejjednodušším případem, kdy je diskriminant nulový. Řešíme tak najednou rovnici 4p² − 36 = 0. Pro jaká p to platí? Toto je ryze kvadratická rovnice a řeší se lehce:

$$\begin{eqnarray} 4p^2-36&=&0\\ p^2-9&=&0\\ p^2&=&9\\ p&=&\pm3 \end{eqnarray}$$

V případě, že je parametr p roven plus nebo minus tři, pak má kvadratická rovnice jedno dvojnásobné řešení.

Nyní vyřešíme, kdy je diskriminant kladný. Řešíme tak kvadratickou nerovnici

$$4p^2-36>0.$$

Už známe nulové body funkce f(p) = 4p² − 36, to jsme vypočítali v předchozím kroku. Z nich poskládáme dva intervaly, jeden „vnitřní“ a druhý „vnější“.

$$\begin{eqnarray} I_1&=&(-\infty,-3)\cup(3, \infty)\\ I_2&=&(-3, 3) \end{eqnarray}$$

V jednom z těchto intervalů je funkce f(p) kladná, ve druhém záporná. Zjistíme to tak, že dosadíme do funkce nějaký bod z jednoho z intervalů. Nejjednodušší je dosadit z intervalu I₂ nulu. Platí, že f(0) = 0 − 36 = −36. V intervalu I₂ je tak funkce záporná, v intervalu I₁ je kladná.

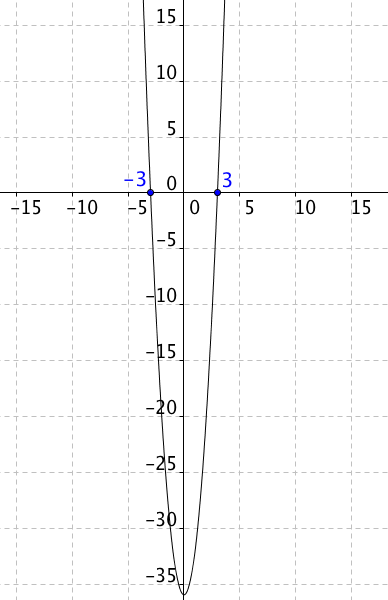
Z toho dostáváme, že v intervalu I₁ má rovnice dvě různá řešení a v intervalu I₂ nemá žádné reálné řešení. Můžete si prohlédnout graf funkce f(p) = 4p² − 36. V bodech plus a minus odmocnina z pěti je nulová, v intervalu I₂ je záporná a v intervalu I₁ je kladná.

Dopočítání kořenů rovnice

Nyní nám zbývá dopočítat řešení rovnice v těch případech, kdy rovnice řešení má. Začneme případem, kdy má rovnice jeden dvojnásobný kořen, tedy když je diskriminant rovný nule. To je v případě, kdy je parametr rovný plus nebo minus odmocnině z devíti.

Případ první, p = 3. Rovnice má pak tvar:

$$x^2+2\cdot3x+9=0.$$

Vypočítáme diskriminant této rovnice. Měl by nám vyjít nulový:

$$D=b^2-4ac=6^2-4\cdot1\cdot9=36-36=0.$$

Dopočítáme kořen podle vzorce:

$$x=\frac{-b\pm\sqrt{0}}{2a}=\frac{-6}{2}=-3.$$

Případ druhý, p = −3. Rovnice má tvar:

$$x^2-2\cdot3x+9=0.$$

Spočítáme diskriminant:

$$D=b^2-4ac=(-6)^2-4\cdot1\cdot9=36-36=0.$$

Dopočítáme kořen:

$$x=\frac{-b\pm\sqrt{0}}{2a}=\frac{6}{2}=3.$$

V posledním kroku už jen dopočítáme, jaká řešení má rovnice, pokud je parametr z množiny (−∞,−3)∪(3, ∞). Diskriminant máme spočítaný, takže dopočítáme kořeny rovnice podle vzorce.

$$x_{1{,}2}=\frac{-b\pm\sqrt{4p^2-36}}{2}=\frac{-b\pm\sqrt{4(p^2-9)}}{2}=\frac{-b\pm2\sqrt{p^2-9}}{2}.$$

Lépe už výraz upravit nejde. Toto jsou tedy kořeny kvadratické rovnice, pokud je parametr z intervalu (−∞,−3)∪(3, ∞). Pokud je parametr z intervalu (−3, 3), pak rovnice nemá reálné řešení.