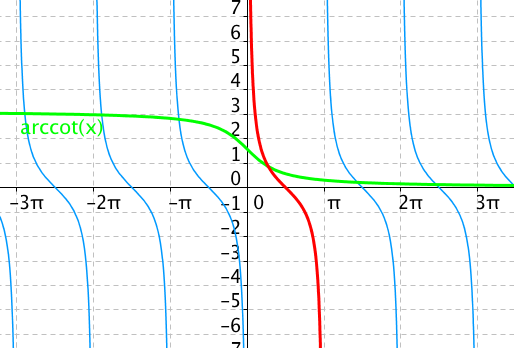
Cyklometrické arcus funkce

Aby měly základní goniometrické funkce smysl, je potřeba definovat také jejich inverzní funkce. Ty se právě nazývají arcus- funkce, přesněji se jedná o arcus sinus, arcus cosinus, arcus tangens a arkus kotangens. Zkráceně také arcsin, arccos, arctan a arccot.

Motivace

Začněme příkladem. Vypočítejte velikost úhlu alfa:

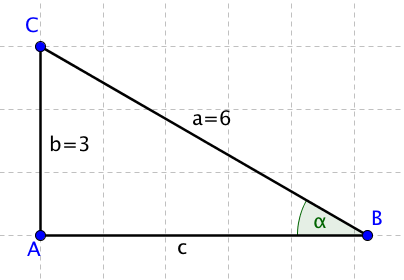
Známe délky dvou stran v trojúhelníku, strany b = 3 a strany a = 6. Máme vypočítat úhel alfa — strana a je přepona a strana b je protilehlá odvěsna k úhlu alfa. S protilehlou odvěsnou pracuje funkce sinus, přesněji řešeno sinus úhlu alfa je roven poměru délky protilehlé odvěsny ku délce přepony. Takže zkusíme dosadit do vzorce:

$$\sin(\alpha)=\frac{|b|}{|a|}=\frac{3}{6}=\frac12$$

Nyní víme, že sinus úhlu alfa je rovný jedné polovině. Otázkou je, jak ze znalosti tohoto čísla získat úhel. K tomu potřebujeme inverzní funkci k funkci sinus. Funkce sinus bere na vstupu úhel a vrátí nám poměr dvou stran. Jenže my nyní potřebujeme funkci, do které vložíme poměr a vypadne nám úhel.

Přesně toto řeší arcus funkce. Ještě než si pořádně nadefinujeme, co to vlastně arcus funkce jsou, tak si dopočítáme příklad pomocí Googlu, který nám říká, že arcsin jedné poloviny je 30 stupňů. Pokud byste si chtěli stejný příklad spočítat na kalkulačce, tak tam často arcus sinus bývá značen jako sin⁻¹.

Inverzní funkce k sinu?

Nejprve si prohlédněte graf funkce sinus:

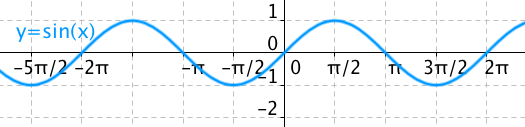
Teď si zopakujeme nějaké vlastnosti ohledně funkcí. Funkce f má inverzní funkci, pokud je prostá. Co to znamená? Že pokud vezmeme dva prvky x₁ a x₁ z definičního oboru, pak musí platit, že jejich obrazy f(x₁) a f(x₂) jsou různé. Toto musí platit pro všechny možné dvojice. Lehce to lze vyčíst z grafu — pokud můžeme graf proložit přímkou, která je rovnoběžná s osou x tak, aby tato přímka protla graf funkce f více než jednou, pak tato funkce není prostá.

Evidentně platí, že u funkce sinus jsme schopni takovou přímku nalézt. Například samotná osa x protíná graf funkce sinus více než jednou, přesněji řečeno protíná ji nekonečně krát. Funkce sinus proto není prostá a tak k ní neexistuje inverzní funkce.

Inverzní funkce k restrikci funkce sinus

Z minulé kapitoly víme, že k funkci sinus neexistuje inverzní funkce. Z první kapitoly ale víme, že existuje nějaká funkce arcsin, která se chová přesně jak požadujeme. Jak jsme toho dosáhli? Vybrali jsme z funkce sinus jen část, která je prostá a můžeme tak k této restrikci funkce nadefinovat inverzní funkci.

Omezení funkce sinus dosáhneme tak, že zmenšíme její definiční obor. Jakou podmnožinu původního definičního oboru (reálná čísla) vybrat? Můžeme vybrat více podmnožin, ale nejlepší volba je interval

$$\left<-\frac{\pi}{2}, \frac{\pi}{2}\right>$$

Tento interval je zobrazen na následujícím obrázku:

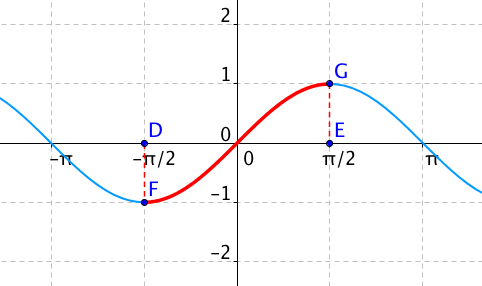
Na tomto definičním oboru již jsme schopni nadefinovat inverzní funkci, protože na tomto intervalu je funkce sinus prostá. Inverzní funkce je souměrná podle osy prvního a třetího kvadrantu s původní funkcí, takže už můžeme narýsovat graf funkce, která bude inverzní k naší restrikci funkce sin(x). Prohlédněte si obrázek:

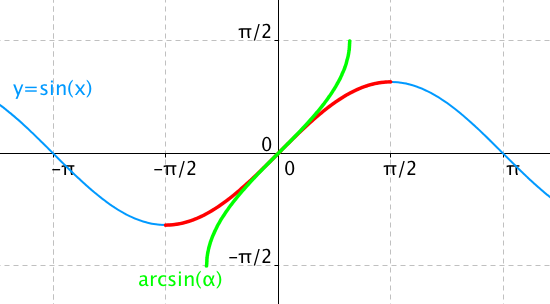
Modře je narýsován původní sinus. Červeně je zvýrazněna část funkce, ke které hledáme inverzní funkci. Zelenou je zobrazena inverzní funkce, kterou značíme arcsin nebo jen asin.

Definiční obor a obor hodnot arcsin

Na těchto dvou funkcích si můžeme hezky ilustrovat prohození definičního oboru a oboru hodnot. Podívejte se na následující obrázek, jsou tam stejné grafy, ve stejných barvách, jen je to trochu zvětšené a přidané nějaké čáry a body:

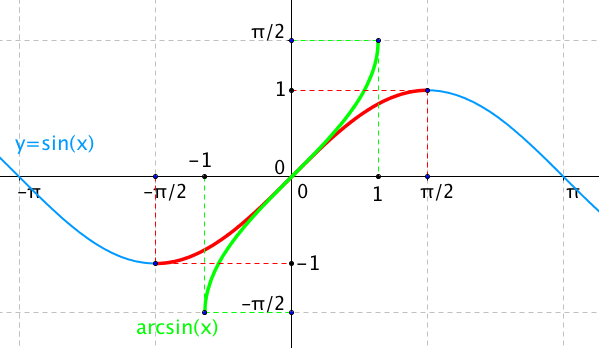
Všimněte si, že definiční obor restrikce funkce sinus (červená čára) byl interval

$$\left<-\frac{\pi}{2}, \frac{\pi}{2}\right>$$

Definičním oborem rozumíme všechna x, pro které je funkce definovaná. My jsme ji definovali právě jen pro tento interval, abychom dostali prostou funkci. Na grafu hledáme tato x na ose x.

Teď se podívejte, jak vypadá obor hodnot funkce arcsin (zelená čára). Obor hodnot jsou všechny y, která nám může funkce vrátit na výstupu, tedy hledáme je na ose y. Funkce arcsin má obor hodnot zase interval

$$\left<-\frac{\pi}{2}, \frac{\pi}{2}\right>$$

toto je obecná vlastnost inverzní funkce, takže by to nikoho nemělo překvapovat. Podobně to platí pro obor hodnot restrikce funkce sinus a pro definiční obor arcsin. Obor hodnot funkce sinus je interval od minus jedné do jedné. sinus nám může vrátit pouze tyto hodnoty, sinus žádného úhly není větší než jedna nebo menší než jedna. A protože sinus žádného úhlu nemůže být větší než jedna, tak je logické, že inverzní funkce také nemůže brát na vstupu hodnotu větší než jedna. Proto je definičním obor funkce arcsin také interval <−1,1>.

Hodnotu funkce arcus sinus si můžete vypočítat ve zdejší kalkulačce.

Arcus cosinus

Teď už jen stručně k inverzní funkci ke cosinu. Ze stejného důvodu jako u funkce sinus zde neexistuje inverzní funkce, protože funkce není prostá. Nicméně můžeme vybrat podmnožinu definičního oboru a získat tak prostou funkci.

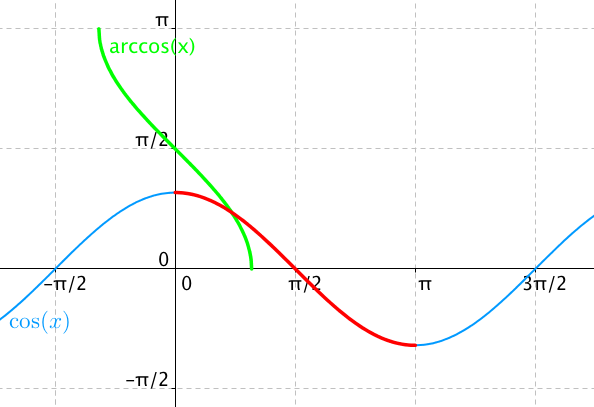
Modře je vyznačen graf funkce cosinus, červená část je pak restrikce této funkce na definiční obor <0,π>. Zelená čára pak představuje graf funkce arccos(x), inverzní funkce k naší restrikci funkce cosinus.

Arcus tangens

Graf funkce tangens vypadá následovně:

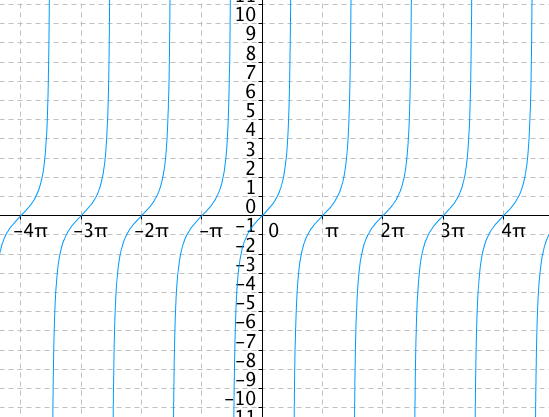
Graf má jiný tvar než předchozí funkce, ale stále není prostý. Opět ale může udělat restrikci této funkce a vybrat takovou část, která prostá bude. Vybereme si interval

$$\left<-\frac{\pi}{2}, \frac{\pi}{2}\right>$$

Inverzní funkce pak má následující tvar:

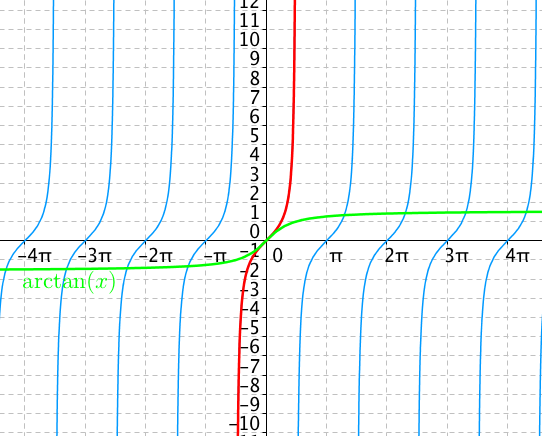
Arcus cotangens

Všechno stejné jako v předchozích odstavcích. Graf funkce cotangens: 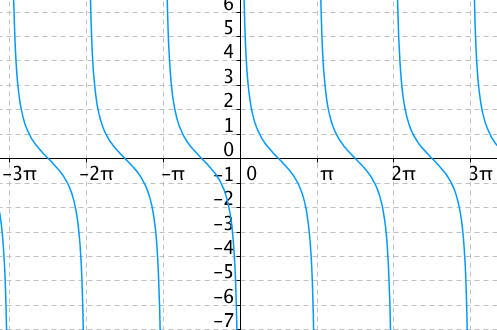Definiční obor restrikce funkce cotangens bude <0,π>.