Sinová a cosinová věta

EU Agency -- individuální doučování a jazyková výuka po celé ČR

Článek je rozdělen do těchto kapitol:

Základní goniometrické funkce

Jednotková kružnice

Cyklometrické Arcus funkce

Sinus, cosinus, tangens a cotangens

Vzorce pro goniometrické funkce

Grafy goniometrických funkcí

Sinová a cosinová věta

Sinová věta je věta, která — narozdíl od běžných goniometrických funkcí — platí v obecném trojúhelníku. Udává nám vztah mezi délkami stran a úhly. Cosinová věta také platí v obecném trojúhelníku a jeho speciálním případem je Pythagorova věta.

Sinová věta

Sinová věta nám říká, že poměr všech délek stran a hodnto sinů jim protilehlých úhlů je v daném obecném (!) trojúhelníku konstatní. Zapíšeme to takto:

$alt: \frac{a}{\sin\alpha}=\frac{b}{\sin\beta}=\frac{c}{\sin\gamma}=2r,$

kde r je poloměr kružnice opsané a a, b a c jsou délky stran trojúhelníku. Předchozí rovnost můžeme také přepsat do tvaru:

$alt: \frac{a}{b}=\frac{\sin\alpha}{\sin\beta}, \frac{b}{c}=\frac{\sin\beta}{\sin\gamma}, \frac{c}{a}=\frac{\sin\gamma}{\sin\alpha}$

Cosinová věta

Cosinová věta také platí v obecném trojúhelníku, stejně jako věta sinová. Cosinová věta zní:

$alt: \parstyle\begin{eqnarray*} a^2 &=& b^2 + c^2 - 2 b c \cdot \cos \alpha\\ b^2 &=& c^2 + a^2 - 2 c a \cdot \cos \beta\\ c^2 &=& a^2 + b^2 - 2 a b \cdot \cos \gamma \end{eqnarray*}$

Všimněte si, že pokud bude jeden z úhlu pravý, tj. bude mít velikost 90 stupňů, pak nám v jednom ze vzorců zmizí poslední část vzorce a dostaneme tvar Pythagorovy věty. Protože pokud α = 90°, pak cos(α) = 0 a tak dostáváme:

$alt: \parstyle\begin{eqnarray*} a^2 &=& b^2 + c^2 - 2 b c \cdot \cos \alpha\\ a^2 &=& b^2 + c^2 - 2 b c \cdot 0\\ a^2 &=& b^2 + c^2 \end{eqnarray*}$

Motivace

Mějme trojúhelník ABC se stranou c o délce |c| = 9. Velikosti úhlů jsou: α = 40°, β = 80°, γ = 60°. Otázka zní, jaká je délka zbývajících dvou stran? V tuto chvíli si již nevystačíme s běžnými goniometrickými funkcemi, protože ty fungují v pravoúhlém trojúhelníku, což tento rozhodně není. Obrázek:

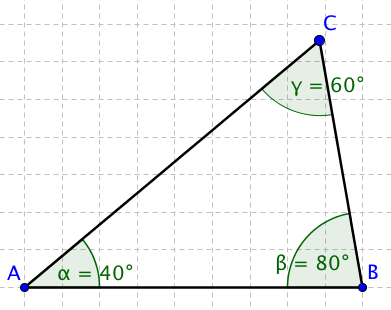
Dopočítejte délky stran a a b

V tuto chvíli budeme muset použít jiné cesty. Jednou z nich je právě sinová věta. Jakým způsobem ji použijeme? Sinová věta nám říká, že:

$alt: \frac{|a|}{\sin\alpha}=\frac{|b|}{\sin\beta}=\frac{|c|}{\sin\gamma}$

My z toho známe všechny úhly a délku strany c. Stranu b tak dopočítáme z rovnosti

$alt: \frac{|b|}{\sin\beta}=\frac{|c|}{\sin\gamma}$

Zde musíme osamostatnit délku strany b. Provedeme ekvivalentní úpravu rovnic a vynásobíme rovnici sinem úhlu beta. Dostaneme:

$alt: |b|=\frac{|c|\cdot\sin\beta}{\sin\gamma}$

Všechny výrazy na prvé straně známe nebo je umíme dopočítat. Takže dosadíme:

$alt: |b|=\frac{9\cdot0,985}{0,866}=10,23.$

Úplně stejným způsobem dopočítáme zbývající stranu a:

$alt: \frac{|a|}{\sin\alpha}=\frac{|c|}{\sin\gamma}$

Osamostatníme |a| vynásobením rovnice sinem úhlu alfa.

$alt: |a|=\frac{|c|\cdot\sin\alpha}{\sin\gamma}$

Dopočítáme výsledek:

$alt: |a|=\frac{9\cdot0,642}{0,866}=6,672$

Odvození věty sinové

Proč sinová rovnost platí? Podívejme se na obyčejný trojúhelník ABC, kde ještě narýsujeme výšku ke straně c.

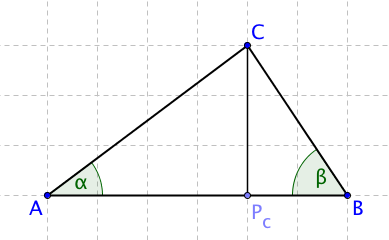
Trojúhelník ABC s výškou ke straně c

Otázka zní, jakou délku má strana CP_c. Díky výšce máme trojúhelník ABC rozdělený na dva pravoúhlé trojúhelníky, pomocí nichž můžeme délku výšky vyjádřit. Zkusíme tak vyjádřit délku strany CP_c pomocí obou trojúhelníků. Platí, že sinus úhlu alfa je roven:

$alt: \sin(\alpha)=\frac{|CP_c|}{|AC|}$

Odtud vyjádříme |CP_c|:

$alt: |CP_c|=\sin(\alpha)\cdot|AC|=\sin(\alpha)\cdot |b|.$

Nyní vyjádříme délku strany CP_c pomocí druhého trojúhelníku, pomocí úhlu beta:

$alt: \sin(\beta)=\frac{|CP_c|}{|BC|}$

Odtud opět osamostatníme |CP_c|:

$alt: |CP_c|=\sin(\beta)\cdot|BC|=\sin(\beta)\cdot |a|$

V tuto chvíli tak máme délku výšky vyjádřenou dvěma vzorci:

$alt: |CP_c|=\sin(\alpha)\cdot |b|=\sin(\beta)\cdot |a|,$

takže dostáváme rovnost

$alt: \sin(\alpha)\cdot |b|=\sin(\beta)\cdot |a|.$

To už je kousek k tomu, co nám říká sinová věta. Celou rovnici vydělíme sinus alfa krát sinus beta:

$alt: \parstyle\begin{eqnarray*} \sin(\alpha)\cdot |b|&=&\sin(\beta)\cdot |a|\quad/:\sin(\alpha)\cdot\sin(\beta)\\ \frac{\sin(\alpha)\cdot |b|}{\sin(\alpha)\cdot\sin(\beta)}&=&\frac{\sin(\beta)\cdot |a|}{\sin(\alpha)\cdot\sin(\beta)}\quad/\mbox{zkratime siny}\\ \frac{|b|}{\sin(\beta)}&=&\frac{|a|}{\sin(\alpha)} \end{eqnarray*}$

V předchozím postupu jsme dokázali část Sinové věty, nicméně důkaz pro ostatní kombinace stran je identický.

Sinová a cosinová věta

Článek je rozdělen do těchto kapitol:

Sinová věta

Cosinová věta

Motivace

Odvození věty sinové

Potřebujete pomoc s příkladem?

Našli jste chybu?

Email (nepovinné):
Text zprávy:
Jaký je 11. měsíc v roce?