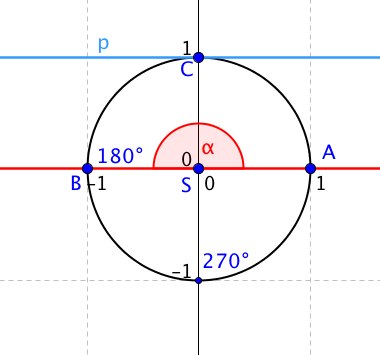
Jednotková kružnice

Jednotková kružnice je obyčejná kružnice, která je bezrozměrná, přesněji poloměr této kružnice je roven jedné. Jednotková kružnice slouží k hezkému znázornění definic jednotlivých goniometrických funkcí.

Pusťte si video verzi článku!

Co je to jednotková kružnice

Jednotková kružnice je kružnice, která má poloměr délky jedné a střed této kružnice se nachází ve středu souřadnicového systémy, tedy v bodě [0, 0]. Podívejte se na následující obrázek:

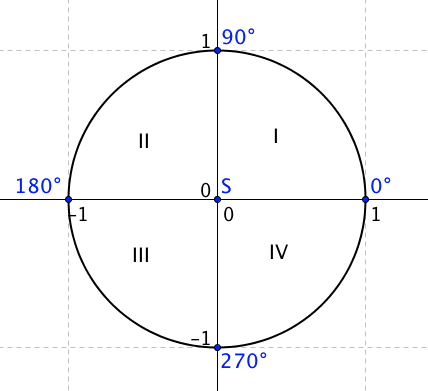
Kružnice je dále rozdělena do čtyř částí, kterým říkáme kvadranty. Vpravo nahoře je kvadrant první, vlevo nahoře druhý, vlevo dole třetí a vpravo dole čtvrtý. Protože tuto kružnici budeme používat k znároňování úhlů, jsou na kružnici zvýrazněny stupně. Tam, kde je nula stupňů, tam obvykle začíná rameno úhlu a směřuje nahoru. Proto je bod [0, 1] označen pravým úhlem.

Definice sinu s cosinu na kružnici

Na jednotkové kružnici se dají velmi hezky znázornit jednotlivé goniometrické funkce. Nejprve na jednotkovou kružnici naneseme nějaký úhel a poté si ukážeme, kde můžeme na jednotkové kružnici přečíst hodnoty jednotlivých funkcí.

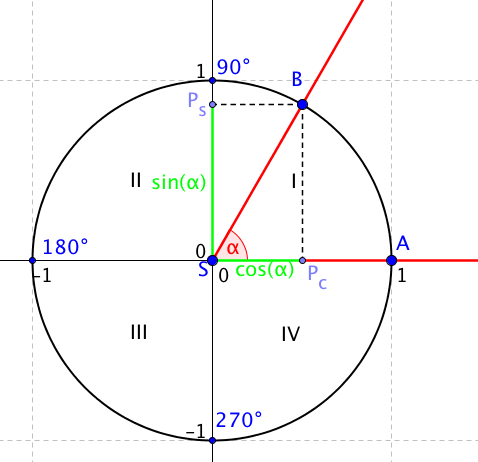
Nanesli jsme na kružnici úhel ASB (červeně). Tento úhel jsme pojmenovali alfa. Ramena úhlu protínají jednotkovou kružnici ve dvou bodech: A a B. Důležitý pro nás bude bod B. Pokud z bodu B povedeme přímku rovnoběžnou s osou x (na obrázku je to ta přerušovaná horizontální čára), tak nám tato přímka protne osu y v právě jednom bodě. Tento bod si označíme P_s. Přitom platí, že délka úsečky SP_s (zelená úsečka) je rovna sinu úhlu alfa.

Protože se pohybujeme v jednotkové kružnici, která má střed v počátku souřadnicového systému, tak platí, že délka úsečky SP_s (zelená úsečka) je rovna y-ové souřadnici bodu P_s což je rovno y-ové souřadnici bodu B.

Na stejné kružnici můžeme přečíst také cosinus. Povedeme tak přímku rovnoběžnou s osou y procházející bodem B. Tato přímka nám protne osu x v bodě, který si označíme P_c. Délka úsečky SP_c je pak rovna cosinu úhlu alfa. Opět můžeme říci, že tato hodnota je rovna x-ové souřadnici bodu B a P_c.

Definice tangensu a kotangensu

Podobně, jako jsme na jednotkové kružnici definovali sinus a cosinus, můžeme zde definovat tangens a kotangens. Pro přehlednost si nejprve ukážeme, kde se na jednotkové kružnici vyskytne tangens. K tomu budeme potřebovat další přímku. Bude to přímka, která je rovnoběžná s osou y a prochází bodem A, neboli bodem [1, 0]. Na následujícím obrázku je to ta modrá přímka:

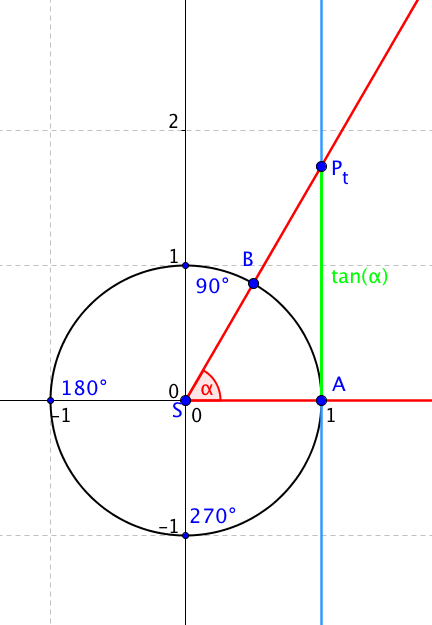
Tato přímka protíná polopřímku (rameno úhlu) SB v jednom bodě, který si označíme P_t. Vzdálenost úsečky AP_t je pak rovna tangensu úhlu alfa. Opět platí, že stačí vzít y-ovou souřadnici bodu P_t a také získáme tangens úhlu alfa.

Abychom na jednotkové kružnici znázornili kotangens, budeme potřebovat ještě jednu přímku. Tentokrát půjde o přímku, která prochází bodem [0, 1] a je rovnoběžná s osou x. Opět je zvýrazněna modrou barvou:

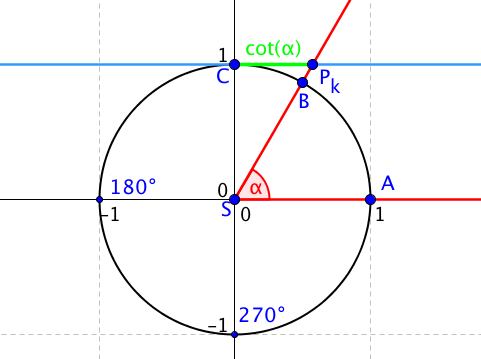
Tato přímka protíná polopřímku (rameno úhlu) SB v jednom bodě, který si označíme P_k. Vzdálenost úsečky CP_k je pak rovna kotangensu úhlu alfa. Jako vždy můžeme vzít pouze x-ovou souřadnici bodu P_k a získáme cotangens úhlu.

Otázkou je, co se stane, pokud bude úhel alfa větší než 90 stupňů u tangensu a větší než 180 stupňů u kotangensu, protože v těchto případech přímka neprotne rameno úhlu, viz následující obrázek:

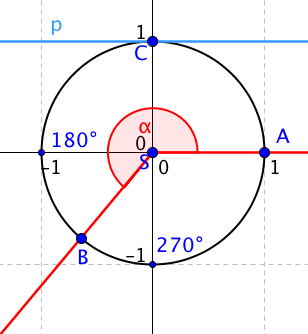
V tuto chvíli uděláme z polopřímky SB přímkou a tato přímka už přímku p protne.

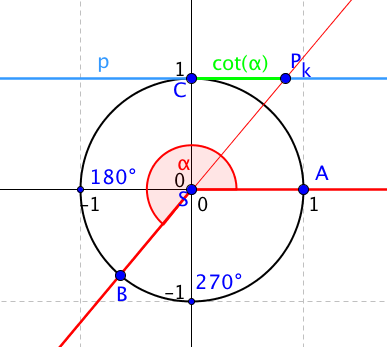
Podobně bychom postupovali i v případě tangensu.

Kdy není tangens a kotangens definovaný

Na jednotkové kružnici si můžeme všimnou jedné zajímavé věci. Pokud je úhel alfa rovný 180 stupňům, potom se přímka p a rameno úhlu nikdy neprotnou, protože budou rovnoběžné. Jak opravíme tento problém? Nijak, kotangens 180 stupňů není definovaný. Podobně není definovaný tangens 90 stupňů, protože takové rameno bude rovnoběžné s osou x a bude tak i rovnoběžné s přímkou, se kterou by se mělo protnout. Následující obrázek to ukazuje alespoň pro kotangens.