Kvadratické nerovnice

Kvadratickou nerovnici můžeme zapsat v obecném tvaru takto: ax² + bx + c > 0 případně ax² + bx + c < 0, kde a, b, c jsou libovolná reálná čísla, a ≠ 0. Namísto „větší než“ a „menší než“ samozřejmě můžeme použít „větší nebo rovno“ a „menší nebo rovno“.

Kladný koeficient a

Takováto nerovnice se řeší podobně jako běžná kvadratická rovnice, nejprve vypočítáme diskriminant a z výsledku můžeme odvozovat další postup. Pokud je diskriminant kladný, má odvozená rovnice dva reálné kořeny. Kořenem rovnice je bod na ose x, ve kterém graf funkce ax² + bx + c protíná osu x. Tyto dva průsečíky nám tak rozdělují osu x na tři intervaly.

Můžeme si zkusit vyřešit nerovnici 2x² − 7x + 3 < 0. Nakreslíme si graf funkce 2x² − 7x + 3, ten vypadá takto:

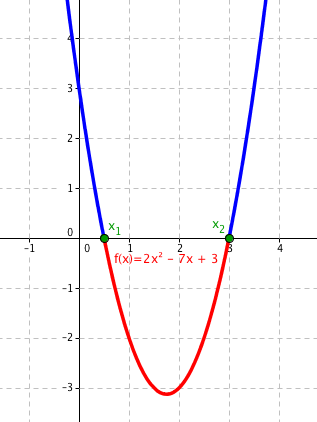
Vidíme, že graf protíná osu x ve dvou bodech: $x_1 = \frac12$ a x₂ = 3. Pokud bychom vypočítali obyčejnou kvadratickou rovnici, získali bychom stejné řešení, protože diskriminant této rovnice je

$$ D = b^2-4ac = (-7)^2-4 \cdot 2 \cdot 3 = 49 - 24 = 25 $$

Kořeny bychom pak vypočítali takto:

$$\begin{eqnarray} x_1 &=& \frac{-b-\sqrt{D}}{2a} = \frac{7-5}{4} = \frac12\\ x_2 &=& \frac{-b+\sqrt{D}}{2a} = \frac{7+5}{4} = 3\\ \end{eqnarray}$$

Tyto dva kořeny nám rozdělují graf funkce 2x² − 7x + 3 na tři intervaly.

• $\left(-\infty, \frac12\right)$ v tomto intervalu jsou hodnoty kladné (graf je „nad“ osou x, moodrá část grafu)
• $\left(\frac12, 3\right)$ v tomto intervalu jsou hodnoty záporné (graf je „pod“ osou x, červená část grafu)
• (3, ∞) v tomto intervali jsou opět hodnoty kladné, zbylá modrá část grafu.

Všimněte si, že v intervalech používáme kulaté závorky, které značí otevřený interval. To znamená, že čísla 3 ani $\frac12$ nejsou obsaženy v intervalu $\left(\frac12, 3\right)$. Je to proto, že v bodě x = 3 má funkce hodnotu nula, a my jsme chtěli vypsat interval, ve kterém jsou hodnoty menší než nula.

Nyní už známe všechny potřebné informace k tomu, abychom určili výsledek nerovnice 2x² − 7x + 3 < 0. Ptáme se, kdy jsou hodnoty funkce 2x² − 7x + 3 menší než nula? Jsou menší než nula v intervalu $\left(\frac12, 3\right)$, červená část grafu.

Můžeme zkusit vyřešit ještě tyto nerovnice:

• 2x² − 7x + 3 ≤ 0: tato nerovnice se od předchozí liší v tom, že je tam ≤ namísto pouhého <. Výsledek bude stejný jako v předchozím případě, pouze místo otevřeného intervalu použijeme uzavřený interval. Výsledkem tak bude interval $\left<\frac12, 3\right>$, protože v bodech $\frac12$ a 3 má funkce 2x² − 7x + 3 hodnotu nula a my nyní hledáme, kdy je tato funkce menší nebo rovna nula. Nezapomínejte, v rovnici je znak ≤.

• 2x² − 7x +3 > 0: výsledkem budou „modré části“ grafu funkce. Výsledné intervaly musíme sjednotit, protože funkce je kladná jak v intervalu $\left(-\infty, \frac12\right)$, tak i v intervalu (3, ∞). Výsledná množina má tvar $\left(-\infty, \frac12\right) \cup \left(3, \infty\right)$.

• 2x² − 7x +3 ≥ 0: opět jsme jen změnili > na ≥. Výsledkem tak bude stejná množina, pouze do ní zahrneme prvky $\frac12$ a 3, couž uděláme uzavřeným intervalem: $\left(-\infty, \frac12\right> \cup \left<3, \infty\right)$.

Záporný koeficient a

Co by se stalo, kdybychom předchozí rovnici změnili na −x² + x + 2 < 0? Hlavní změna se udála v koeficientu a, který je teď roven a = −1. V minulé rovnici jsme měli 2x², koeficient před x² byl kladný, zatímco zde je záporný. Nejlepší bude, když se podíváme na graf:

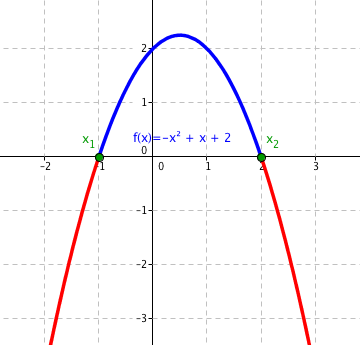
Vidíme, že graf se změnil především tak, že už nemá tvar písmene „U“, ale má tvar kopce. Na postupu se ale nic nezměnilo. Opět vznikají tři intervaly:

• (−∞, −1): hodnoty jsou záporné.
• (−1, 2): hodnoty jsou kladné.
• (2, ∞): hodnoty jsou záporné.

Výsledkem nerovnice −x² + x + 2 < 0 tak bude sjednocení intervalů (−∞, −1) ∪ (2, ∞).

Ale já si nechci pořád čmárat grafy!

Nemusíš! Všechna předcházející řešení byla založená na tom, že jsme si nakreslili graf a z nich jsme vyčetli body průniku s osou x a následně i to, jestli jsou v daném intervalu hodnoty kladné, nebo záporné. Jde to ale i jinak.

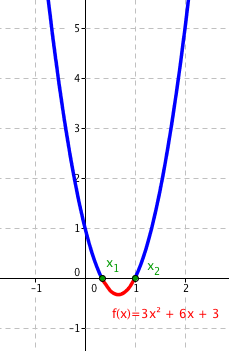
Pokud máme kvadratickou rovnici 3x² − 4x + 1 < 0, můžeme jen vyřešit kvadratickou rovnici 3x² − 4x + 1 = 0 klasickými způsoby. Vypočítáme tak diskriminant:

$$ D = b^2-4ac=(-4)^2-4\cdot3\cdot1=4 $$

Dále vypočítáme kořeny kvadratické rovnice:

$$\begin{eqnarray} x_1 &=& \frac{-b - \sqrt{D}}{2a} = \frac{4-2}{6} = \frac13\\ x_2 &=& \frac{-b + \sqrt{D}}{2a} = \frac{4+2}{6} = 1\\ \end{eqnarray}$$

Víme, že graf protíná osu x v bodech $x_1=\frac13$ a x₂ = 1. Vznikají nám tři intervaly: $\left(-\infty, \frac13\right)$, $\left(\frac13, 1\right)$, (3,∞). Otázkou je, jak zjistit, jestli má funkce f(x) = 3x² − 4x + 1 v daném intervalu kladné, nebo záporné hodnoty.

To zjistíme tak, že do funkce f(x) = 3x² − 4x + 1 vždy vložíme nějaké číslo z daného intervalu. Pokud bude výsledek funkce kladný, je na celém intervalu funkce kladná. Totéž pro záporné hodnoty.

• Vybereme libovolné číslo z intervalu $\left(-\infty, \frac13\right)$, například nulu, s ní se dobře počítá. S nulou zavoláme funkci f: f(0) = 3 · 0² − 4 · 0 + 1 = 1. Číslo 1 je kladné, v tomto intervalu jsou tak kladné hodnoty.

• Vybereme číslo z intervalu $\left(\frac13, 1\right)$: nejlepší je asi jedna polovina:

  $$f(\frac12) = 3\left(\frac12\right)^2-4\frac12+1=3\frac14-2+1=-\frac14$$

  Číslo $-\frac14$ je záporné, takže v tomto intervalu jsou všechny hodnoty záporné.

• V posledním intervalu budou stejné hodnoty jako v prvním — kladné. Vždy se to střídá: kladné — záporné — kladné nebo záporné — kladné — záporné. Ale můžeme si to klidně dopočítat. Zvolíme číslo z intervalu (3,∞), například 10:

  $$ f(10) = 3\cdot10^2-4\cdot10+1=300-40+1=261 $$

  To je kladné číslo, všechny hodnoty v tomto intervalu tak jsou kladné.

Zbývá dořešit celou nerovnici. Ta měla tvar: 3x² − 4x + 1 < 0. Na základě předchozích informací víme, že funkce 3x² − 4x + 1 má záporné hodnoty v intervalu $\left(\frac13, 1\right)$. Už jen pro ověření se můžeme podívat na graf:

Nulový diskriminant

Při řešení kvadratické rovnice nám může vyjít nulový diskriminant. Ten vyjde vy chvíli, kdy se graf funkce dotýká osy x v jednom bodě. Ukážeme si to na nerovnici 3x² + 6x + 3 ≥ 0. Diskriminant je roven nule:

$$ D = b^2 - 4ac = 6^2 - 4 \cdot 3 \cdot 3 = 36 - 36 = 0 $$

Graf by vypadal takto:

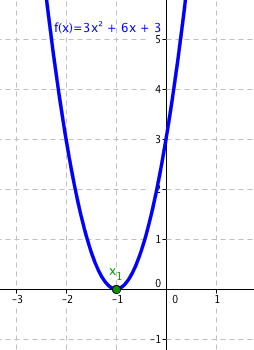
Jak je vidět, graf protíná osu x v jediném bodě x₁ = −1 a zbytek grafu je nad osou x v kladných hodnotách. To znamená, že řešením nerovnice 3x² + 6x + 3 ≥ 0 je celá množina reálných čísel, protože ať dosadíme za x jakékoliv reálné číslo, vždy bude hodnota větší nebo rovna nule.

Záporný diskriminant

Pokud nám vyjde diskriminant záporný, znamená to, že graf nikdy neprotíná osu x. Jak se to projeví v našich nerovnicích? Tak, že graf je buď celý nad osou x nebo celý pod osou x. Pokud bychom předchozí rovnici upravili takto: 3x² + 6x + 4 > 0 (změnili jsme znaménko z ≥ n > a změnili jsme číslo tři na čtyři), tak by diskriminant vyšel:

$$ D = 6^2 - 4 \cdot 3 \cdot 4 = -12 $$

a graf by vypadal takto:

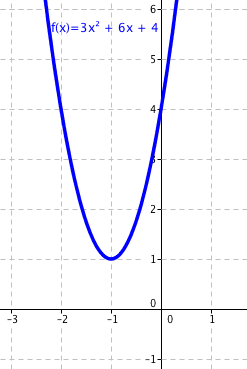
Graf je kompletně celý nad osou x, ať za x dosadíme jakékoliv reálné číslo, výsledná hodnota bude vždy kladná. řešením nerovnice tak je opět množina reálných čísel.