Určitý integrál

Určitý integrál slouží k měření velikosti plochy obrazců, které jsou popsány nějakou funkcí.

Motivace

Mějme dánu funkci $f(x) = \sin(x) + \frac{x}{4}$. Nyní bychom se mohli zeptat — jak velká je plocha pod křivkou grafu od bodu a = 0 do bodu b = 10? Zajímá nás tak velikost plochy, která je ohraničena osou x, křivkou grafu funkce f a vertikálními přímkami v bodech x₁ a x₂. Vše shrnuje obrázek:

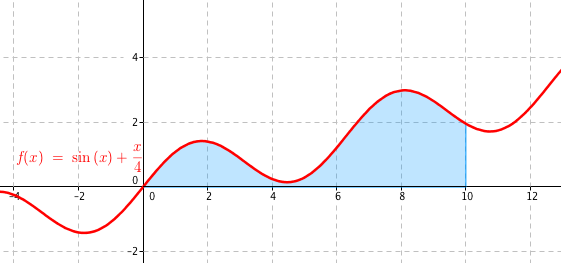
Zajímá nás velikost modře zvýrazněné plochy. Jak bychom ji určili? Můžeme postupovat tak, že rozdělíme celou modrou plochu na několik menších ploch a poté spočítáme obsahy těchto menších sploch a všechny tyto dílčí obsahy sečteme. Abychom vypočítali obsah menších ploch, musí tato menší plocha mít nějaký rozumný tvar, abychom obsah spočítali pomocí nějakého vzorce. Nabízí se obdélník.

Jako první zvolíme rostoucí posloupnost bodů x₀ až x_n takových, že x₀ = a, x_n = b. Čím větší n, tím přesnější výsledek dostaneme. Zvolíme jednoduchou posloupnost x₀ = 0, x₁ = 1, x₂ = 2, …, x₁₀ = 10. Ze sousedních bodů vytvoříme intervaly <x_i, x_{i + 1}>, tj. získáme množinu intervalů

$$ D = \left\{\left<0, 1\right>, \left<1, 2\right>, \left<2, 3\right>, \ldots, \left<9, 10\right>\right\} $$

První interval označíme D₁, druhý D₂, atd. Dále nalezneme minimální hodnoty funkce f v každém intervalu D_i. Například v D₁ má funkce f minimální hodnotu pro x = 0 a f(0) = 0. V D₂ je nejnižší hodnota v bodě x = 1 a $f(1)=\sin(1)+\frac14 \approx 1,0914$. Atd. Tyto funkční hodnoty si označíme. Nejnižší funkční hodnotu v intervalu D_i označíme m_i. Takže $m_1 = 0, m_2 \approx 1,0914$ atd.

Nyní do grafu zakreslíme obdélníky. i-tý obdélník bude mít šířku x_i − x_{i − 1} a výšku m_i:

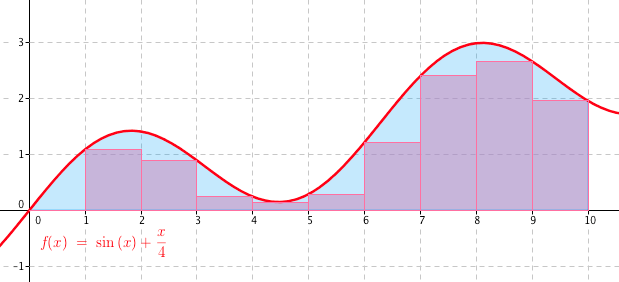
Vidíme, že každému intervalu náleží jeden obdélník, který je celý pod křivkou, ale zároveň je nejvyší. Výška každého obdélníku v i-tém intervalu je právě m_i. Pokud bychom nyní sečetli obsahy těchto obdélníků, získali bychom přibližný odhad velikost plochy pod křivkou. Čím více obdélníků pod křivku nakreslíme, tím přesnější odhad získáme. Obsah i-tého obdélníku bychom vypočítali jako s_i = m_i · x_i − x_{i − 1}, takže součet všech obdélníků by pak byl:

$$ s = \sum_{i=1}^{10} m_i \cdot x_i - x_{i-1} $$

Můžeme postupovat opačně: místo toho, abychom brali vždy minimální funkční hodnotu na intervalu D_i, vezmeme největší funkční hodnotu. Tyto funkční hodnoty bychom označili M_i. Obdélníky by pak vypadaly takto:

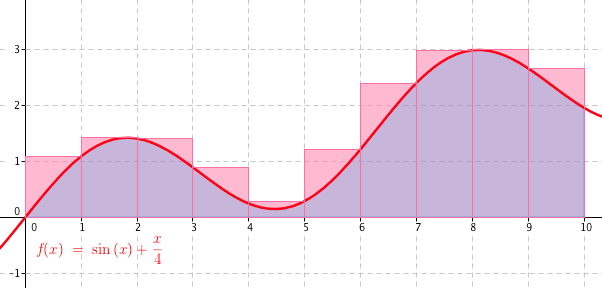
Opět každému intervalu náleží jeden obdélník a ten má vždy výšku M_i. Horní stěna obdélníku se křivky dotýká vždy jen v lokálních maximech daného intervalu. Sečtením obsahů jednotlivých obdélníků bychom získali další odhad velikosti obsahu plochy pod křivkou. Tento obsah bychom spočítali jako

$$ S = \sum_{i=1}^{10} M_i \cdot x_i - x_{i-1} $$

Opět platí, že pokud bychom zvětšili počet obdélníků, získáme přesnější odhad.

Zavedeme pojmy dolní a horní integrální součet. Řekneme, že s(D, f) je dolní integrální součet a jeho hodnota je rovna

$$ s(D, f) = \sum_{i=1}^{10} m_i \cdot x_i - x_{i-1}, $$

kde f je spojitá funkce na intervalu <a, b>, kde x₀ = a, x_n = b, D je dělení funkce do intervalů a n je počet těchto intervalů. Horní integrální součet označíme S(D, f) a je roven:

$$ S(D, f) = \sum_{i=1}^{10} M_i \cdot x_i - x_{i-1}, $$

kde f je funkce a D dělení funkce do n intervalů.

Přitom ale, zjednodušeně řečeno, platí, že čím větší je D, tím více jsou si hodnoty s(D, f) a S(D, f) blíže, až se budou někde v nekonečnu rovnat. Platí tak, že existuje jediné reálné číslo A takové, že

$$ s(D, f) \le A \le S(D, f) $$

pro všechna možná dělení D. Co je A za číslo? Číslo A je právě obsah plochy pod křivkou, protože to je jediná hodnota, která je větší nebo rovna součtu obsahů obdélníků pod křivkou a zároveň menší nebo rovna než součet obsahu obdélníků „nad křivkou“.

Definice určitého integrálu

Z předchozí kapitoli víme, že pro spojitou funkci f na intervalu <a, b> platí s(D, f) ≤ A ≤ S(D, f) pro všechna dělení D. Toto číslo A se nazývá určitý integrál funkce f od a do b. Používáme pak označení

$$ A = \int_a^b f(x) \mathrm{d}x. $$

Newton-Leibnizova formule nám dále říká, že platí tento vztah:

$$ \int_a^b f(x) \mathrm{d}x = F(b)-F(a), $$

kde F je primitivní funkce k funkci f. Pravá část rovnice se občas zapisuje i takto:

$$ \int_a^b f(x) \mathrm{d}x = \left[F(x)\right]_a^b $$

Geometrický význam určitého integrály je pak již zmíněný obsah plochy pod křivkou nezáporné funkce f. Začali jsme funkcí $f(x) = \sin(x) + \frac{x}{4}$, takže si zkusíme spočítat obsah plochy v intervalu <0, 10>. Spočítáme tak určitý integrál

$$ \int_0^{10} \sin(x) + \frac{x}{4} \mathrm{d}x $$

Jako první zintegrujeme funkci f:

$$\begin{eqnarray} \int \sin(x) + \frac{x}{4} \mathrm{d}x &=& \int \sin(x) \mathrm{d}x+ \int \frac{x}{4} \mathrm{d}x\\ &=& -\cos(x) + c_1 + \frac{x^2}{8} + c_2 \\ &=& \frac{x^2}{8} - \cos(x) + c_1+c_2 \end{eqnarray}$$

Pritimitivní funkce F tak má tvar $F(x) = \frac{x^2}{8} - \cos(x) + c$. Rozepíšeme určitý integrál:

$$\begin{eqnarray} \int_0^{10} \sin(x) + \frac{x}{4} \mathrm{d}x &=& F(10) - F(0)\\ &=& \frac{10^2}{8} - \cos(10) + c - \left(\frac{0^2}{8} - \cos(0) + c\right)\\ &=& \frac{100}{8} - \cos(10) + \cos(0) + c - c\\ &\approx& 12{,}5 + 0{,}839 + 1\\ &\approx& 14{,}339 \end{eqnarray}$$

Přibližný obsah plochy pod křivkou na intervalu <0, 10> je 14,339.