Rozložení pravděpodobnosti
Rozložení nebo rozdělení pravděpodobnosti náhodné proměnné nám udává, jaká je pravděpodobnost, že náhodná proměnná bude mít zrovna danou hodnotu.
Rozdělení diskrétní proměnné
Mějme nějakou diskrétní náhodnou proměnnou, například bychom mohli sledovat, kolik půllitrů piv za den vypije místní ochlasta Bambula. Sledováním Bambuly celý jeden měsíc jsme sestrojili následující tabulku:
| Den | Půllitrů piva | Den | Půllitrů piva | Den | Půllitrů piva |
|---|---|---|---|---|---|
| 1. | 5 | 11. | 10 | 21. | 4 |
| 2. | 10 | 12. | 5 | 22. | 6 |
| 3. | 4 | 13. | 12 | 23. | 10 |
| 4. | 4 | 14. | 10 | 24. | 10 |
| 5. | 5 | 15. | 12 | 25. | 4 |
| 6. | 4 | 16. | 12 | 26. | 5 |
| 7. | 0 | 17. | 6 | 27. | 10 |
| 8. | 5 | 18. | 10 | 28. | 5 |
| 9. | 4 | 19. | 6 | 29. | 0 |
| 10. | 5 | 20. | 10 | 30. | 10 |
Vidíme, že se Bambula z kraje měsíce ještě trochu šetřil, ale pak už do sebe házel jedno pivo za druhým. A ten týden od 11. dne musel být šílený. Označme si tuto náhodnou diskrétní proměnnou X. Nyní nás bude zajímat, jaká je pravděpodobnost toho, že Bambula za nějaký jeden den v měsíci vypije právě x půllitrů piva.
Než si spočítáme samotnou pravděpodobnost, sestrojíme obyčejný graf četnosti. Najdeme si všechny půllitry piv, které Bambula v nějaký den vypil a zaneseme je do grafu četnosti. Například deset půllitrů vypil Bambula celkem devětkrát, takže pro hodnotu deset půllitrů budeme mít sloupeček s hodnotou devět:
Graf čteme tak, že Bambula vypil šest půllitrů tři dny v měsíci.
Jaká je pravděpodobnost, že Bambula za den vypil deset půllitrů? Formálně bychom to zapsali takto: pravděpodobnostní funkci označíme P a dotaz na deset půllitrů bychom zapsali takto: P(X = 10). Tím se ptáme, jaká je pravděpodobnost, že náhodná proměnná X nabývá hodnoty deset?
Pravděpodobnost se bude rovnat relativní četnosti dané hodnoty. Takže si ještě sestrojíme graf relativní četnosti:
Nyní můžeme říci, že P(X = 10) je rovno 0,3, tedy 30 %.
Statistická vs. matematická pravděpodobnost
Vezměme si pro příklad klasickou hrací kostku. Zkusme s ní 600krát hodit. Z hlediska klasické matematické pravděpodobnosti máme stejně velkou šanci, že nám padne jednička, dvojka, …, šestka. Každá stěna kostky má pravděpodobnost hodu $\frac16$. Čistě teoreticky by nám tak každá strana měla padnout přesně stokrát, když jsme házeli kostkou šestsetkrát.
To se samozřejmě nejspíše nestane. V našem experimentu můžeme získat tyto výsledky:
| Číslo na kostce | Počet hodů | Relativní četnost |
|---|---|---|
| 1 | 105 | 0.175 |
| 2 | 103 | 0.171666 |
| 3 | 90 | 0.15 |
| 4 | 96 | 0.16 |
| 5 | 100 | 0.16666 |
| 6 | 106 | 0.17666 |
Vidíme, že relativní četnost, a tedy i pravděpodobnost, výskyty jedné tečky na kostce je 0.175, což je 17,5 %. To je sice blízko pravděpodobnosti $\frac16$, což je 0,16666…, ale není to úplně přesné.
Neznamená to, že by jedna nebo druhá pravděpodobnost byla špatná. Sestavit naprosto dokonale vyváženou kostku není vůbec lehký úkol, stejně tak může být obtížné provést samotný test, kdy kostkou 600krát hodíme.
Matematická pravděpodobnost tak funguje za ideálních podmínek, kdy bychom kostkou házeli do nekonečna. Čím déle bychom ideálně vyváženou kostkou házeli, tím více by se relativní četnosti jednotlivých hodů přibližovaly teoretické matematické pravděpodobnosti.
Proto rozlišujeme dvě pravděpodobnosti — matematickou, která vychází ze zidealizovaných podmínek, a statistickou (též empirickou), kterou vypočítáme z relativních četností z našich dat.
Abychom spočítali statistickou pravděpodobnost, měli bychom mít k dispozici dostatečně velký soubor dat. Například našeho opilce Bambulu jsme sledovali pouze jeden měsíc, mnohem lepší by ale bylo, kdybychom ho sledovali alespoň rok.
Rozdělení spojité proměnné
U spojité proměnné neurčujeme pravděpodobnost v určité bodě, ale vždy jen v intervalu. Pravděpodobnost bude rovna velikosti plochy pod křivkou, takže k výpočtu budeme potřebovat integrál. Můžeme mít takový graf spojité proměnné, může se jednat například o měření nějaké odchylky v cm:
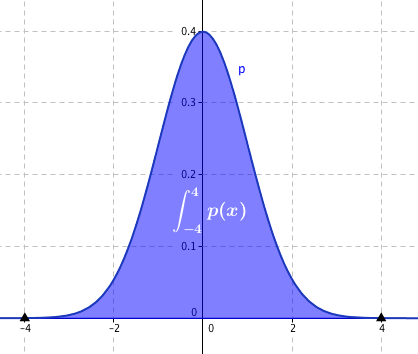
Na ose x tak máme hodnoty v cm, na ose y máme relativní četnosti. Dejme tomu, že jsme naměřili jen hodnoty v intervalu <−4, 4>. Empirická pravděpodobnost, že naměříme odchylku v tomto intervalu je tak 1, tj. 100 %.
Jak s tím souvisí plocha? Řekneme, že velikost plochy $\int_{-4}^4 p(x)$ , kde p je funkce pravděpodobnosti, nám udává právě těch 100 %. Pokud bychom se zeptali, jaká je empirická pravděpodobnost, že bude hodnota v intervalu <0, 4>, dostali bychom takový obrázek:
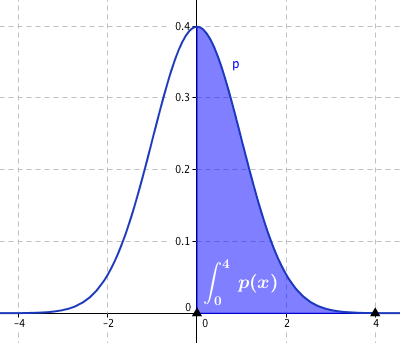
Předchozí zvýrazněná část odpovídala 100 %, tato odpovídá 50 %, protože obsah je evidentně poloviční. Přesně bychom statistickou pravděpodobnost vyjádřili jako poměr
$$ \frac{\int_{-4}^4 p(x)}{\int_{0}^4 p(x)}. $$
Zákon velkých čísel
S předchozí kapitolou souvisí známý zákon velkých čísel. Ten neformálně říká to, že při velkém počtu nezávislých pokusů se bude statistická pravděpodobnost blížit relativním četnosti.
Můžeme si to znova představit na hodu mincí. Může nám padnout panna nebo orel, každá strana má pravděpodobnost $\frac12$, 50 %. Pokud čtyřikrát hodíme mincí, může nám padnout třikrát panna a jednou orel. Relativní četnost je tak $\frac34$ a $\frac14$. To je poměrně daleko od $\frac12$.
Pokud hodíme celkem desetkrát, může nám padnout sedmkrát panna a třikrát orel. To jsou četnosti $\frac{7}{10}$ a $\frac{3}{10}$. To má sice pořád daleko do $\frac12$, ale pořád jsou tato čísla blíže k jedné polovině než předchozí četnosti.
Takhle bychom mohli pokračovat dále. Kdybychom hodili tisíckrát mincí, mohla by nám padnout 520krát panna a 480krát orel. To už jsou četnosti $\frac{13}{25}$ a $\frac{12}{25}$, které už se hodně blíží jedné polovině (pro představu $\frac{13}{25} = 0,52$).
Všimněte si, že přestože jsou relativní četnosti daleko blíže od jedné poloviny, tak absolutní četnosti jsou od „ideální“ četnosti mnohem dále. Když jsme hodili kostkou desetkrát, byla ideální absolutní četnost u každé strany 5. Tedy že nám pětkrát padne panna a pětkrát orel. Protože nám panna padla sedmkrát, dává to rozdíl dvou hodů: 7 − 5 = 2. Hodili jsme „o dva hody jinak“ než by nastalo v ideální situaci.
Když jsme ale hodili mincí tisíckrát, padla panna 520krát, což dává rozdíl 20 hodů od ideálu, protože v ideálním případě měla každá strana padnout 500krát. Zdálo by se tak, že čím vícekrát hodíme, tím vzdálenější výsledky dostaneme.
To ale nijak nevadí, zákon velkých čísel netvrdí, že se budou blížit k ideálu absolutní četnosti, ale relativní. A ty se blíží. Tedy v absolutních četnostech se budou možná vzdalovat, ale v relativním se budou přibližovat.