Kružnice

Kružnice je křivka, která má od daného bodu, středu kružnice, vždy stejnou vzdálenost. Kružnice se také řadí mezi kuželosečky.

Popis kružnice

Prohlédněte si obrázek kružnice:

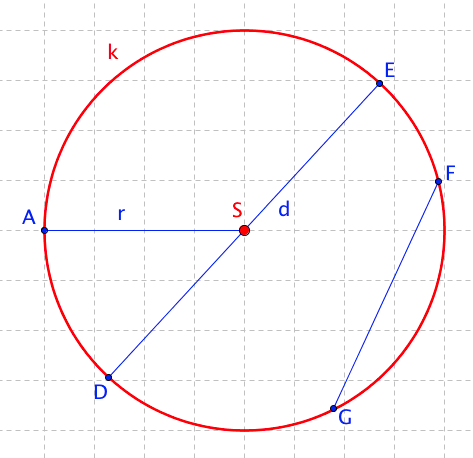
Kružnici obvykle značíme malým písmenem k nebo l.

• Každá kružnice má střed, označuje se S.
• Všechny body kružnice mají od středu S stejnou vzdálenost, říká se jí poloměr kružnice a označujeme ho r. Na obrázku se jedná o úsečku AS.
• Úsečka, která spojuje dva různé body na kružnici se nazývá tětiva. Na obrázku úsečka FG.
• Tětiva, která prochází středem S se nazývá průměr kružnice a označuje se d. Platí, že 2r = d.

Dále mluvíme o vnitřní a vnější oblasti kružnice. Vnitřní oblast je množina všech bodů, která mají vzdálenost od středu menší než poloměr kružnice. Vnější oblast jsou všechny body, které mají vzdálenost od středu větší než je poloměr. Pokud sjednotíme kružnici a vnitřní oblast kružnice, dostaneme kruh.

Obvod a obsah

Jaký je vztah mezi průměrem kružnice a obvodem kružnice? Kolikrát je obvod kružnice větší než jeho průměr? Pokud si vezmete nějaký kruh a zkusíte změřit jeho průměr a následně obvod, zjistíte, že přibližně třikrát. Přesněji 3,1415-krát a ještě přesněji π-krát.

Číslo π (čteme pí) se nazývá Ludolfovo číslo. Je to iracionální číslo, tedy číslo s nekonečným desetinným rozvojem bez periody. Pokud tak máte pevně daný průměr kružnice jako nějaké celé číslo, její obvod nikdy nezjistíte zcela přesně. V praktickém životě ale bohatě stačí znát nějakou přibližnou hodnotu.

Vzorec pro obvod kružnice vypadá takto:

$$o=\pi d=2\pi r$$

Vzorec pro obsah kruhu:

$$S=\pi r^2$$

Vzájemné polohy dvou kružnic

• Soustředné kružnice mají společný střed S. 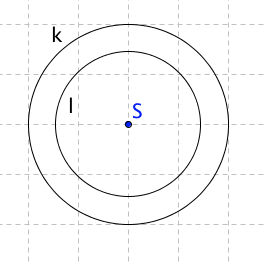Nesoustředné kružnice jsou pak takové kružnice, které nemají společný střed. Úsečka, která spojuje jejich středy se nazývá středná úsečka.

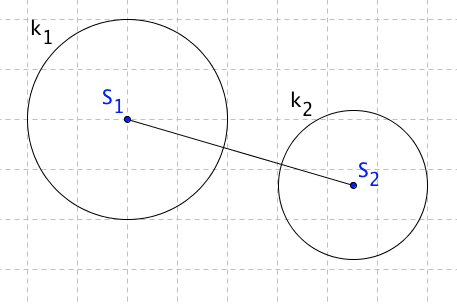
• Kružnice k₁ leží ve vnější oblasti k₂, kružnice nemají žádný společný bod.

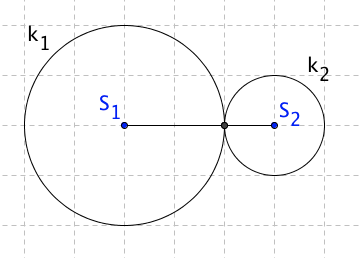
• Kružnice k₁ leží ve vnější oblasti k₂, ale dotýkají se v jednom bodu.

• Kružnice se protínají ve dvou bodech.

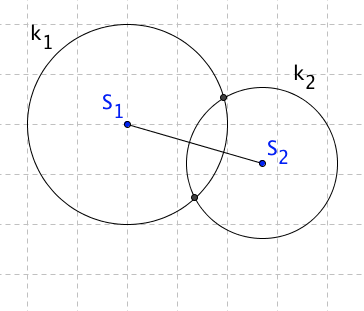
• Kružnice k₁ leží ve vnitřní oblasti k₂ a dotýkají se v jednom bodě.

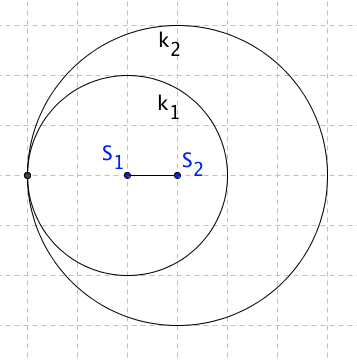
• Kružnice k₁ leží ve vnitřní oblasti k₂.

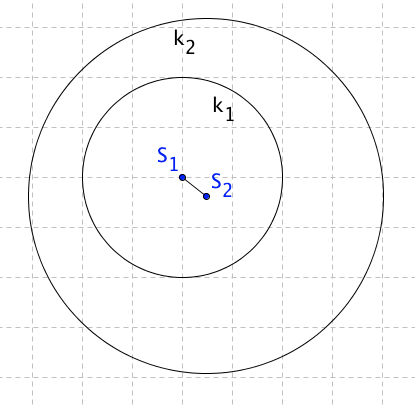
Oblouky

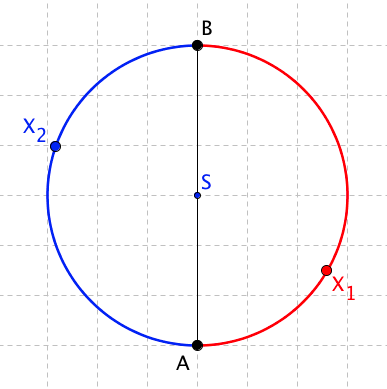
Každá tětiva, která má krajní body A a B, rozdělí kružnici na dvě části zvané oblouky. Každý bod na kružnici, krom bodů A a B je pak vnitřním bodem jednoho z oblouků. Oblouk poté značíme například AXB, kde X je vnitřním bodem oblouku.

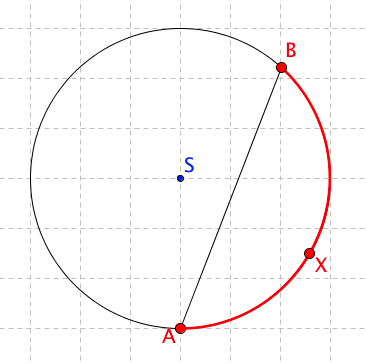
Jestliže je tětiva zároveň průměrem, rozdělí kružnici na dva shodné oblouky, kterým říkáme polokružnice nebo půlkružnice. V opačném případě se kružnice vždy rozdělí na dva různě velké oblouky.

Středový úhel

Mějme kružnici k se středem v bodě S a oblouk AB. Pak úhel ASB nazýváme středovým úhlem nad obloukem AB. Nad menším obloukem se nachází konvexní středový úhel (úhel je menší než $180^{\circ}$), nad větším obloukem je nekonvexní úhel (více než $180^{\circ}$).

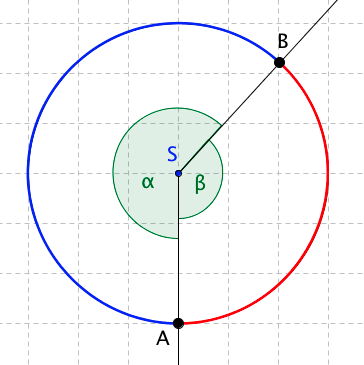
Kružnice na obrázku má vyznačeny dva oblouky AB. Většímu oblouku přísluší úhel α, menšímu β.

Obvodový úhel

Mějme kružnici k se středem v bodě S a oblouk AB. Dále si zvolme bod V, který nenáleží tomuto oblouku, ale nachází se na kružnici. Pak úhel AVB se nazývá obvodový úhel.

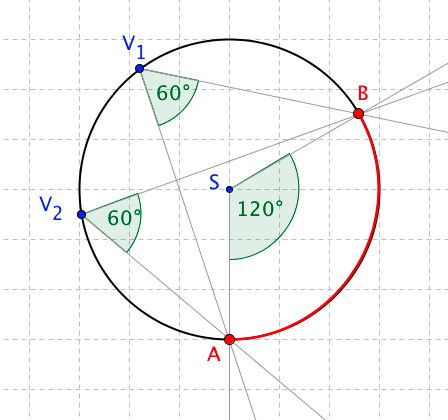
Na obrázku jsou dva obvodové úhly, AV₁B a AV₂B. Všimněte si, že oba mají stejnou velikost — $60^{\circ}$ — a že tato velikost je poloviční oproti středovému úhlu — $120^{\circ}$.