Přenášení úhlu

Máte-li nějaký úhel a chcete tento úhel zkopírovat někde jinde, mžůete použít metodu přenášení úhlů.

Jak přenést úhel

Začneme s tímto obrázkem:

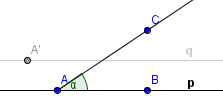
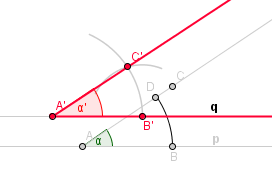
Naším úkolem je přenést úhel α o fous výš tak, aby vrchol přenešeného úhlu α' odpovídal bodu A', aby měl stejnou orientaci a aby spodní rameno leželo na přímce q (v horním obrázku je zašedlá). Nyní budeme potřebovat kružítko. Narýsujeme část kružnice mezi rameny úhlu α o libovolném poloměru se středem ve vrcholu úhlu, A. V kružítku si ponechejte poloměr této kružnice.

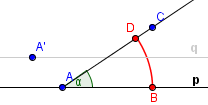
Nyní narýsujte stejnou část kružnice, o stejném poloměru, ale se středem v bodě A', tedy v místě, kde má být vrchol přenášeného úhlu. Tam, kde kružnice protne přímku q, se bude nacházet bod B'.

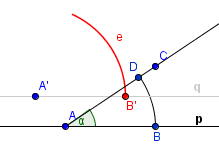
Nyní vezmeme do kružítka vzdálenost úsečky |BD|, zabodneme kružítko do bodu B' a narýsujeme kružnici. V bodě, kde tato kružnice protne předchozí část kružnice, se nachází bod C'.

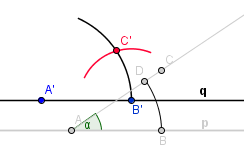
Nyní už máme všechny tři body potřebné k sestrojení nového úhlu B'A'C'.

Sčítání a odečítání úhlů

Pokud máte dva úhly, které potřebuje sečíst, můžete použít tento postup. Vezmete jeden úhel, přenesete ho k druhému tak, aby měly jedno společné rameno a výsledný úhel tvoří ramena, která mají ty dva úhly různá:

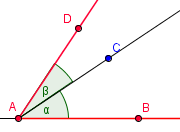
V tomto příkladu je znázorněn součet α + β. Společné rameno polopřímka AC a různá ramena polopřímky AB a AD. Výsledek je úhel BAD.

U odečítání to funguje velice podobně, akorát jeden úhel nepřenesete vně druhého úhlu, ale dovnitř úhlu. Poté od většího úhlu jakoby odečtete průnik těch dvou úhlů a máte rozdíl.

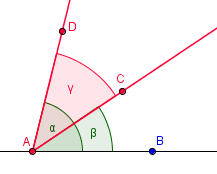
Obrázek znázorňuje rozdíl α − β. Červená část pak opět zvýrazňuje výsledný úhel.