Úhel

Máte-li nějaký úhel a chcete tento úhel zkopírovat někde jinde, můžete použít metodu přenášení úhlů.

Co je to úhel

Definice úhlu není úplně jednoduchá záležitost a existují různé verze. Ale pro naše potřeby by mohla postačit tato varianta: Úhel je část roviny ohraničená dvěma polopřímkami, která mají společný počátek. Na této definici je důležité, že úhel nejsou pouze ta dvě ramena, nýbrž celá ta plocha, celá rovina, kterou ty dvě ramena svírají. Viz následující obrázek:

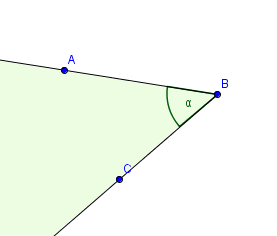
Předchozí obrázek ale nebyl zcela pravdivý, protože jsme nespecifikovali, jaký úhel myslíme. Na první pohled bychom si sice mohli pod úhlem ABC představit zmíněnou plochu, ovšem stejně tak bychom si mohli představit druhou část roviny:

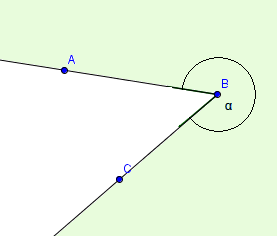
Proto bychom při zapisování úhlů měli rozlišit, zda myslíme konvexní úhel (ten, který má méně než $180^{\circ}$) či nekonvexní úhel (více než $180^{\circ}$). Nekonvexnímu úhlu můžeme také říkat konkávní úhel. To se může zapisovat například za pomoci orientovaného úhlu.

Úhel může mít buď kladnou nebo zápornou orientaci. U kladné orientace postupujeme proti směru hodinových ručiček a v záporném po směru hodinových ručiček. Takže při zápisu úhlu ABC je jako první zmíněna polopřímka AB a jako druhá polopřímka BC. V kladném směru se koukneme na polopřímku AB a postupujeme dále proti směru hodinových ručiček. V našem příkladu nahoře by nám vyšel první obrázek, konvexní úhel. Kdybychom si určili záporný směr, dostali bychom úhel nekonvexní, tedy druhý obrázek. Standardně se počítá s kladným směrem, i v tomto článku budou zápisy psány v kladném smyslu.

Úhel se tedy skládá ze dvou ramen, které úhel ohraničují, z vrcholu úhlu, z něhož ty polopřímky vycházejí a z plochy, kterou vymezují ramena úhlu. Máme-li úhel ABC, ramena úhlu jsou AB a BC a vrchol je B.

Velikost úhlu

Stejně jako můžeme změřit délku úsečky, můžeme také změřit velikost úhlu. Ta se měří buďto v klasické stupňové míře, kterou určitě znáte nebo v obloukové míře. Stupňová míra je jednoduchá, $90^{\circ}$ je pravý úhel (například vnitřní úhly čtverce mají každý $90^{\circ}$), $180^{\circ}$ je přímý úhel (svírají ho třeba opačné polopřímky) a $360^{\circ}$ je plný úhel (svírají ho polopřímky, které leží na sobě — takovýto úhel je tvořen celou okolní rovinou). Stupeň se dále dělí na minuty (značí se ′) a vteřiny (značí se ″). Jeden stupeň má 60 minut a jedna minuta má šedesát vteřin. $1^{\circ} = 60′$ a 1′ = 60″.

Obrázky jednotlivých úhlů:

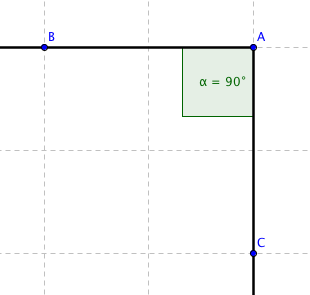
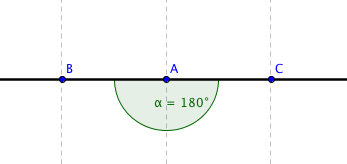
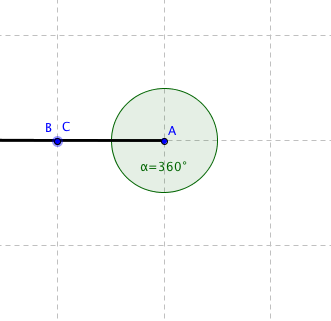
Oblouková míra už je trochu horší na představivost, protože se zde počítá s radiány, které nemají absolutní hodnotu. Velikost radiánu a další vlastnosti už jsem ale popisoval u goniometrických funkcí, takže se nebudu opakovat.

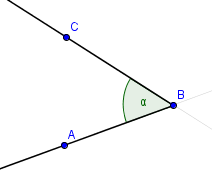
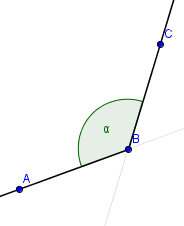
Úhly můžeme dále podle velikosti rozdělit na ostrý úhel, který má méně než $90^{\circ}$ a na tupý úhel, ten má mezi $90^{\circ}$ a $180^{\circ}$. Jedná se o jakousi podmnožinu konvexního úhlu, který jsem ukazoval výše. Více než $180^{\circ}$ má nekonvexní úhel, který se ji dále nedělí.

Dvojice úhlů

Některé specifické dvojice úhlů mají různé vlastnosti, o kterých je dobré vědět.

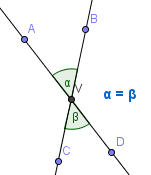
• Vrcholové úhly jsou takové úhly, které mají společný vrchol a jejich ramena tvoří opačné polopřímky. Vrcholové úhly jsou vždy shodné, mají stejnou velikost.

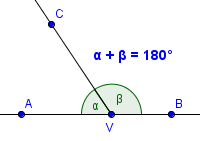
• Vedlejší úhly jsou takové úhly, které mají jedno rameno společné a druhá ramena jsou opačné polopřímky. Součet vedlejších úhlů je vždy roven $180^{\circ}$, přímému úhlu.

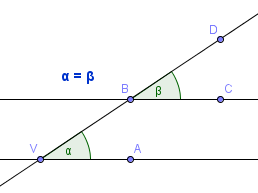
• Souhlasné úhly jsou úhly, jejichž první ramena jsou rovnoběžná a druhá leží na jedné přímce. Musí také platit, že úhly mají stejnou orientaci. Souhlasné úhly jsou shodné.

Existují ještě další typy úhlů, ale už jsou to pouze pozice, které se dají odvodit na základě těchto tří výše popsaných umístění.

Operace s úhly

S úhly můžeme provádět jisté elementární operace. Nejzákladnější je sčítání. Numericky na tom není takřka co zkazit, normálně sečtete velikosti úhlů. Pokud má úhel více než 360°, obvykle se převádí na jednodušší tvar, někde v intervalu $0^{\circ} - 360^{\circ}$. Zkrátka jako byste pracovali v třistašedesátkové číselné soustavě. Podobně pokud máte v příkladu minuty či vteřiny, musíte počítat v šedesátkové soustavě (jako normální hodiny).

Takže pro jistotu jeden ukázkový příklad. Sečtěte tyto úhly: $\alpha = 183^{\circ} 51′$ a $\beta = 222^{\circ} 24′$. Nejprve spočítáme minuty $51′ + 24′ = 75′ = 1^{\circ} 15′$ (postup je jednoduchý, vydělíte 75 šedesáti. Výsledek udává počet stupňů a zbytek počet zbývajících minut). Nyní spočítáme stupně: $183^{\circ} + 222^{\circ} = 405^{\circ}$. K tomuto dílčímu výsledku přičteme předchozí výsledek $405^{\circ} + 1^{\circ} 15′ = 406^{\circ} 15′$. Nyní tento úhel budeme snižovat o 360 tak dlouho, dokud nebude v intervalu mezi 0 a 360. Snižujeme proto, že pokud opíšeme úhel o velikosti $360^{\circ}$, jsme opět na začátku, úhel o velikosti $361^{\circ}$ bude mít na papíře stejnou velikost jako úhel o velikosti $1^{\circ}$. Dostáváme se k tomuto výpočtu: $406^{\circ} 15′ = 46^{\circ} 15′$.

• Wikipedie