Čtverec
Čtverec je základní geometrický útvar, který má čtyři stejně dlouhé strany a každý vnitřní úhel má velikost právě 90 stupňů. Existuje také metoda, které se říká metoda doplnění na čtverec.
Popis
Příklad čtverce si můžete prohlédnout na následujícím obrázku.
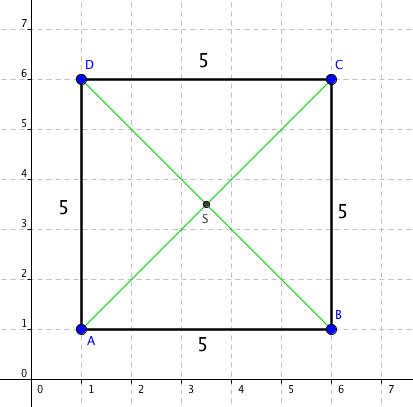
Každý čtverec se skládá ze čtyř vrcholů, náš obsahuje vrcholy A, B, C, D. Na obrázku jsou označeny modře. Mluvíme v tom případě o čtverci ABCD. Tyto vrcholy jsou spojeny úsečkami tak, že tvoří čtyři strany čtverce. Konkrétně jde o strany: AB, BC, CD, DA. Na obrázku jsou tyto strany vyznačeny tučnými čárami. Každá z těchto stran má stejnou délku, konkrétně délku pět.
Každá strana svírá se svými sousedními strana pravý úhel, tedy úhel o velikosti 90 stupňů.
Úhlopříčky čtverce
Zelenými úsečkami jsou vyznačeny úhlopříčky. Každý čtverec má dvě úhlopříčky, tento má úhlopříčky AC a DB. Úhlopříčka je tak úsečka, která spojuje dva protilehlé vrcholy čtverce. Další fakta o úhlopříčkách:
- Úhlopříčka e vžjdy delší než strana čtverce.
- Přesněji: pokud má strana čtverce délku a, pak úhlopříčka u má délku $|u|=a\cdot\sqrt{2}$. Je to jen aplikace Pythagorovy věty.
- Úhlopříčky se vždy protínají ve středu čtverce (v těžišti).
- Úhlopříčka daný čtverec dělí na dvě poloviny. Obě úhlopříčky pak čtverec dělí na čtyři čtvrtiny.
- Samotné úhlopříčky se navzájem půlí. Pokud vyznačíme střed čtverce bodem S (jako na obrázku), pak délka úsečky AS bude stejná jako délka úsečky CS.
- Úhlopříčka dělí úhel mezi přilehlými stranami. Například na obrázku má úhel ABC velikost 90 stupňů a úhel ABD má velikost 45 stupňů.
- Úhlopříčky svírají mezi sebou pravý úhel.
Obvod a obsah
Obvod je délka okraje čtverce, tedy součet délek všech stran. Platí tak, že pokud má čtverec strany délky a, pak obvod je roven 4 · a. Obsah je velikost plochy, kterou čtverec zabírá. Vezmete délku jedné strany a vynásobíte ji délkou sousedící strany. Ale protože má čtverec všechny strany stejně dlouhé, můžete jen vynásobit a · a. Ještě jednou souhrnně:
$$\begin{eqnarray} (\mbox{obvod})\quad o &=&4\cdot a\\ (\mbox{obsah})\quad S&=&a\cdot a=a^2 \end{eqnarray}$$
Pro příklad: čtverec na předchozím obrázku má obvod 4 · 5 = 20 a obsah 5 · 5 = 25.
Poloha čtverce
Je následující útvar čtverec?

Předchozí útvar je čtverec, protože má čtyři strany, všechny stejně dlouhé a každá strana svírá s každou sousedící pravý úhel. Pokud čtverec natočíme, stále zůstane čtvercem. Pokud ale například změníme velikosti úhlů, pak už to čtverec nebude:
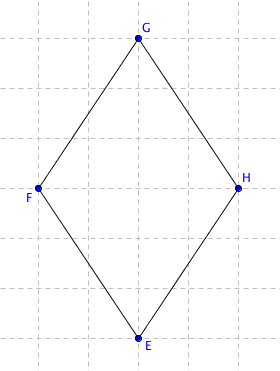
Čtyři vrcholy, čtyři stejně dlouhé strany, ale všechny úhly nejsou pravé, takže se nejedná o čtverec.
Jak narýsovat čtverec
Čtverec se rýsuje snadno a přímočaře. Jediné, co potřebujete znát, je délka strany. Pokud je délka strany třeba tři centimetry, tak jako první narýsujete úsečku o délce tři centimetry. Označíte krajní body jako vrcholy A a B (nebo jak chcete). Potom musíte pomocí pravítka odměřit pravý úhel a narýsovat dvě kolmé úsečky z bodů A a B směrem, kterým chcete. Úsečky budou mít opět délku tři. Nové body označte C a D. Nakonec spojte úsečkou body C a D.
Kružnice opsaná a vepsaná
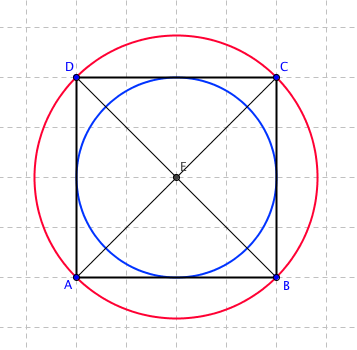
Kružnice opsaná a vepsaná jsou dva pojmy, které se spolu se čtverci vyskytují. Obě kružnice mají střed ve středu čtverce, tedy v průniku úhlopříček.
Kružnice opsaná je kružnice, která protíná všechny vrcholy čtverce. Má poloměr AS, kde A je vrchol čtverce (libovolný) a S je střed.
Kružnice vepsaná je kružnice, která se dotýká všech stran čtverce. Má poloměr a/2, kde a je délka strany čtverce.
Metr čtvereční
Se čtvercem souvisí i základní jednotka pro obsah, což je právě metr čtvereční. Co to znamená? Pokud řekneme, že něco má plochu jeden metr čtvereční, znamená to, že ta plocha má stejný obsah, jako čtverec, který má délku strany jeden metr. Pokud máte pokoj o ploše 10 metrů čtverečních, znamená to, že se tam těch čtverců o straně délky jeden metr, vleze deset. Pozor, neznamená to obsah čtverce o délce strany 10 metrů! Přehledně to zobrazuje následující obrázek:
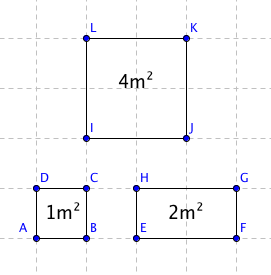
Pokud byste vzali čtverec o straně s délkou 10 metrů, pak by se jednalo o jednotku ar. Pokud čtverec o délce strany 100 metrů, pak by to byl hektar.
