Objemy a obsahy
Nejdříve hodně stručně k teorii, kdyby náhodou někdo nevěděl. Obvod tělesa je součet délek všech jeho stran, vyjadřuje se v metrech a odvozených jednotkách. Obvod se obvykle značí písmenkem O. Obsah tělesa je velikost plochy, které těleso tvoří, počítá se v metrech čtverečních, matematicky se čtvereční metr vyjadřuje pomocí dvojky v horním indexu: m2. Obsah se běžně zapisuje písmenkem S. Objem je prostor, které těleso tvoří, jednoduše řečeno to vyjadřuje, kolik vody tam můžete nalít. Objem se počítá v metrech krychlových a odvozených jednotkách a prostorové míry se zapisují pomocí trojky v horním indexu: m3. Objem se běžně zapisuje pomocí písmene V. Obsah a objem můžeme vyjádřit i v dalších (a v běžném životě asi používanějších) jednotkách jako je ar nebo hektar pro obsah a litr pro objem. Pro další informace o jednotkách se podívejte na web jednotky.cz. Obsah či objem lze obecně spočítat integrály.
Čtverec a obdélník
Obě tělesa jsou dvouprostorová, tudíž zde nalezeneme pouze obvod a obsah. U čtverce je to všechno nejjednodušší, protože čtverec už z definice má všechny strany stejně dlouhé. Tudíž počítáme-li obvod čtverce, stačí nám vzít jednu stranu čtverce a vynásobit ho čtyřmi (počtem stran): O=4a. Obvod obdélníku je pouze o fous složitější. Obdélník má vždy dvě a dvě stejně dlouhé strany, tudíž se nabízí dvě cesty: buď všechny strany jednoduše posčítat anebo vzít délky dvou různých stran, vynásobit je dvěma a sečíst: O=2a+2b.
Obsah čtverce není o nic složitější než jeho obvod. Vezmete jeho jednu stranu a vynásobíte druhou stranou. Vzhledem k tomu, že čtverec má všechny strany stejně dlouhé, vzniká vzorec: S = a·a = a2. Obdélník funguje zcela identicky jako čtverec, pouze s tím rozdílem, že obdélník nemá všechny strany stejně dlouhé a proto musíte násobit dvě různé na sebe kolmé strany: S=a·b.
Rovnoběžník
Rovnoběžník je útvar, který je podobný obdélníku, ale má dvě protější strany zkosené, viz obrázek pod tímto odstavcem. Obvod rovnoběžníku je jednoduchý a v zásadě stejný jako u obdélníku: O=2a+2b, nicméně obsah už je trošku zajímavější. Abychom spočítali obsah rovnoběžníku, musíme z něj udělat obdélník, jinak to nepůjde. A jak z něj uděláme obdélník nám ukazuje následující obrázek:

Nejprve odřízneme přebývající část rovnoběžníku (vybarvená část) a přiděláme ji na druhou stranu rovnoběžníku, čímž nám vznikne obdélník:
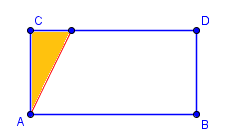
Teprve teď můžeme snadno vypočítat obsah rovnoběžníku, vzoreček bude stejný jako v případě obdélníku. Nicméně grafický převod rovnoběžníku není pohodlný, používá se prostý vzoreček, který vychází právě z toho převodu. Strana a bude totiž identická jak v případě obdélníku, tak v případě rovnoběžníku, liší se jen druhá strana. My tedy u rovnoběžníku namísto strany b budeme počítat s výškou rovnoběžníku, která se rovná straně b v upraveném obdélníku. Přehledně to ukazuje následující obrázek (násobit budeme červeně zvýrazněné strany):
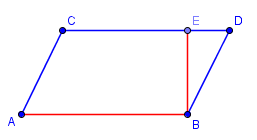
Vzorec vypadá takto: S=va·a.
Lichoběžník
Obvod je jasný, spočteme všechny strany dohromady. Obsah lichoběžníku už je větší oříšek. Teoreticky bychom mohli postupovat stejně jako v případě rovnoběžníku, nicméně nevíme, jestli máme vzít tu delší (AB) nebo tu kratší (CD) stranu.

Proto se použije finta – vypočítáme průměrnou délku těch dvou rovnoběžných stran a budeme počítat s ní. Sečteme tedy délku strany AB a CD, vydělíme dvěma a pak již počítáme stejně jako v případě rovnoběžníku – vynásobíme to ještě výškou a máme obsah. S=(a+c)/2 · va.
Trojúhelník
Trojúhelník je dvojrozměrné těleso a jako takové tudíž u něj můžeme počítat obvod a obsah, nemůže mít a také nemá objem. Obvod trojúhelníku spočítáme tak, že sečteme všechny jeho strany. Tedy obecný vzorec by vypadal takto: O=a+b+c. Samozřejmě můžeme nalézt speciální případy, třeba je jasné, že rovnostranný trojúhelník má všechny strany stejně dlouhé a tudíž nám stačí znát délku jedné strany a ten vynásobit třemi. Pak by ten vzorec vypadal takhle: O'=3a.
Na obsah trojúhelníku budeme potřebovat jednu malou úpravu. Abychom mohli spočítat obsah trojúhelníku, musíme z něj udělat rovnoběžník (podobně, jako jsme z rovnoběžníku dělali obdélník). Jak z trojúhelníku udělat rovnoběžník nám opět ukazuje následující malůvka:
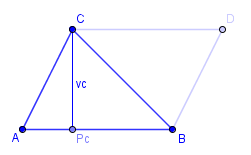
Z tohoto obrázku už by mělo být jasné, jak spočítat obsah trojúhelníku – budete postupovat stejně, jako kdybyste počítali obsah rovnoběžníku, akorát výsledek vydělíte dvěma: S=(va·a)/2
Kruh
Kruh je specifický útvar v tom, že u něj obvod ani obsah nejde vypočítat. Tedy alespoň ne s absolutně přesnou hodnotou. Ať už chceme s kruhem počítat cokoliv, snad nikdy se neobejdeme bez konstanty Pí – π. Přesná hodnota π není známá, jedná se o iracionální číslo, nicméně jeho přibližná hodnota, se kterou se obvykle počítá (pokud nemáte jeho hodnotu uloženou v kalkulačce), je 3,14.
Nyní přejděme ke vzorečkům. Už dávni myslitelé zjišťovali, jak vypočítat obvod kruhu, respektive kružnice (kružnice je pouze ta čára, oblouk, kružnice nemá vnitřek a nemá tedy ani obsah, kdežto kruh má obsah, neboť se do něj započítává i vnitřek kružnice). Zjistilo se, že poměr průměru kruhu (který lze snadno změřit) k obvodu kruhu je vždy stejný a postupem času se i spočítalo, kolikrát je obvod kruhu větší než jeho průměr. A světe div – je to právě Pí krát. Obvod kruhu tedy spočítáme O=π·d=2·π·r (častěji se uvádí ten druhý, složitější vzorec, protože většinou spíše známe poloměr než průměr), kde d je průměr a r je poloměr kruhu.
Obsah kruhu je pak S=π·r2, nevím, co víc bych k tomu řekl :-).
Krychle a kvádr
Toto jsou první prostorová tělesa, u nich tedy budeme určovat obsah povrchu a objem. Vzhledem k tomu, že krychle má šest stěn a všechny stěny tvoří čtverce, je postup jasný: vypočítáte obsah jedné stěny a ten následně vynásobíte šesti. S=6a2. U kvádru je to již zdlouhavější, protože má vícero různých stěn. V zásadě stačí spočítat obsah tří různých stěn, sečíst a vynásobit dvěma a máte obsah povrchu kvádru: S=(a·b + b·c + a·c)·2.
Objem krychle se počítá na chlup stejně jako obsah čtverce jen s tím drobným rozdílem, že nesmíme zapomenout, že se nacházíme v prostoru. Zkrátka stačí vzít délku strany a umocnit ji na třetí: V=a3. U kvádru je to podobné, jen musíme ty tři strany násobit zvlášť, protože jsou různě dlouhé: V=a·b·c.
Koule
Obsah povrchu koule (=kulová plocha) se vypočítá S=4·π·r2 a objem koule je V=4/3·π·r3. Jestli si chcete přečíst docela složité odvození výpočtu objemu koule, koukněte se na Cavalieriův princip. Odvození velikost povrchu koule je pak například na zdejším fóru.
Válec
Obsah povrchu válce vypočteme jako součet obsahů dvou podstav s obsahem stěny. Podstava je normální kruh, takže obsah jedné podstavy bude roven obsahu kruhu, tedy obsah jedné podstavy vypočteme takto:
$$S_p=\pi\cdot r^2$$
Stěna válce není nic jiného, než „srolovaný“ obdélník, kde délka jedné strany je rovna výšce válce (označíme v) a druhá je rovná obvodu kružnice u podstavy. Takže obsah stěny je roven:
$$S_s=v\cdot2\pi r$$
Obsah povrchu celého válce tak je roven:
$$S=2\cdot S_p+S_s=2\pi r^2+2v\pi r=2\pi r(r+v)$$
Objem válce je jednodušší, je výška vynásobená obsahem podstavy. Obsah podstavy už jsme počítali v předchozím kroku. Výsledek:
$$V=v\cdot\pi r^2$$
Jehlan a kužel
Obsah povrchu jehlanu se obecně počítá jako součet obsahu podstavy a obsahů všech stěn. Obecný vzorec na to moc není. Objem jehlanu má něco společného s výpočtem obsahu trojúhelníku – vezmete obsah podstavy a vynásobíte ho výškou jehlanu. Výsledek následně vydělíte třemi a máte objem jehlanu. V=(Sp · v)/3, kde Sp je obsah podstavy.
Povrch rotačního kužele se rovná součtu obsahu podstavy a obsahu pláště. Obsah podstavy je jasný, jedná se o obyčejný kruh, tedy S=π·r2. Obsah pláště je trochu složitější, musíte si představit, že ten plášť „rozvinete“ na stůl a tím vám vznikne jakási kruhová výseč, jejíž obsah se rovná: S=π·r·s, kde s je poloměr pláště (vzdálenost vrcholu kužele od hrany podstavy, v podstatě je to něco podobného jako hrana u jehlanu). Objem kužele je V=(π · r2 · h)/3, kde h je výška kužele.
Příklad na obsahy
Spočítejte obsah následujícího obrazce (předpokládejte, že míry na ose jsou v metrech):
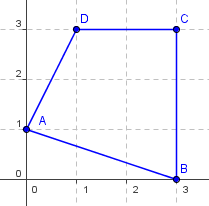
Na první pohled zjistíme, že toto těleso je jakýsi obecný mnohoúhelník, na který jako celek nemůžeme aplikovat žádný vzorec. Musíme ho tedy rozdělit na menší části, které již dokážeme spočítat. Nejschůdnější bude, pokud ze spodní části uděláme trojúhelník a z vrchní části lichoběžník. Rozdělení ukazuje následující obrázek:
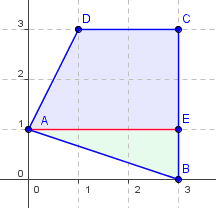
Teď spočítáme obsah trojúhelníku ABE podle vzorce S=(a · va)/2. Stranou a bude v tomto případě strana AE a výškou na tuto stranu bude strana EB. Vidíme, že |AE|=3 m a |EB|=1 m. Dosazením do vzorce získáváme: S=(3 · 1)/2=1,5 m2.
V druhém kroku spočítáme obsah lichoběžníku a to podle vzorce S=(a+c)/2 · va. Strana a bude v našem případě strana AE a strana c strana DC. Výšku opět lehce vyčteme z obrázku, jedná se o délku úsečky EC. Dosazením do vzorečku získáváme: S=(3+2)/2 · 2=5 m2.
Předchozí dva dílčí výsledky pouze sečteme a máme výsledný obsah tělesa. S=1,5 m + 5 m = 6,5 m2.
Spočítejte obsah následujícího obrazce (předpokládejte, že míry na ose jsou v metrech):
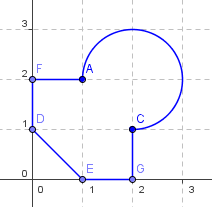
Asi je opět na první pohled patrné, že jeden vzoreček nám stačit nebude a že budeme muset obrazec nějakým způsobem upravit. Budeme to počítat následujícím způsobem: Vypočítáme obsah toho „čtverce“, přičteme k tomu tři čtvrtiny obsahu kruhu a odečteme ten malý trojúhelník, vlevo dole:
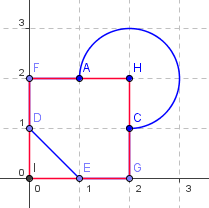
Obsah čtverce vypočítáme jednoduše: S1 = 2 · 2 = 4 m2. V druhém kroku spočítáme obsah kruhu. Opět pouze dosadíme do vzorečku a spočítáme S2 = π · 12 · 3/4 = 3π/4. Zbývá už jen spočítat obsah trojúhelníku DEI a odečíst ho od obsahu čtverce. Strana EI i její výška DI mají shodně délku 1 m, takže obsah trojúhelníku bude S3 = ½.
V posledním kroku sečteme a odečteme dílčí výsledky: S = S1 + S2 − S3 = 3,5 m2 + 3π/4 m2.
