Euklidovy věty

Starý alexandrijský matematik Eukleidés sestavil dvě věty týkající se trojúhelníků, konkrétně se týkají výšky a odvěsny.

Euklidova věta o výšce

Tato věta funguje pouze na pravoúhlém trojúhelníku. Podívejme na základní zadání:

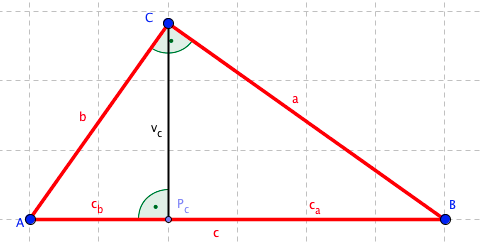
Máme zde trojúhelník ABC, strana c je přepona, úsečka v_c je výška ke straně c. Bod P_c nám rozděluje stranu c na dvě úsečky: úsečku AP_c si označíme c_b a úsečku BP_c si označíme c_a.

Euklidova věta o výšce pak říká, že platí vztah

$$ v_c^2 = c_a \cdot c_b, $$

kde v_c značí délku úsečky v_c atp. Jinými slovy: pokud bychom sestavili čtverec o délce strany v_c a obdélník o délkách c_a a c_b, pak by tyto útvary měly stejný obsah. Podívejte se na následující obrázek, ve kterém je právě takový čtverec a obdélník zvýrazněn:

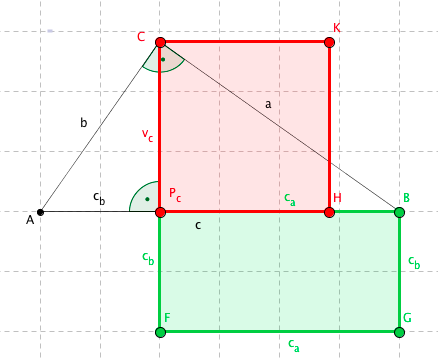
Euklidova věta o výšce říká, že tyto útvary mají stejný obsah. Červený čtverec má délku strany v_c, zelený obdélník má délku jedné strany rovnou c_a a délka druhé strany je rovná c_b.

Důkaz Euklidovy věty o výšce si můžete přečíst na Wikipedii.

Euklidova věta o odvěsně

I tato druhá Euklidova věta platí v pravoúhlém trojúhelníku. Zůstaneme u prvního obrázku trojúhelníku:

Druhá věta pak tvrdí, že

$$\begin{eqnarray} a^2 &=& c \cdot c_a\\ b^2 &=& c \cdot c_b\\ \end{eqnarray}$$

Pokud sestrojíme čtverec o velikosti strany a, pak tento čtverec bude mít stejný obsah jako obdélník o délkách stran c a c_a. Opět si můžete čtverec a obdélník prohlédnout:

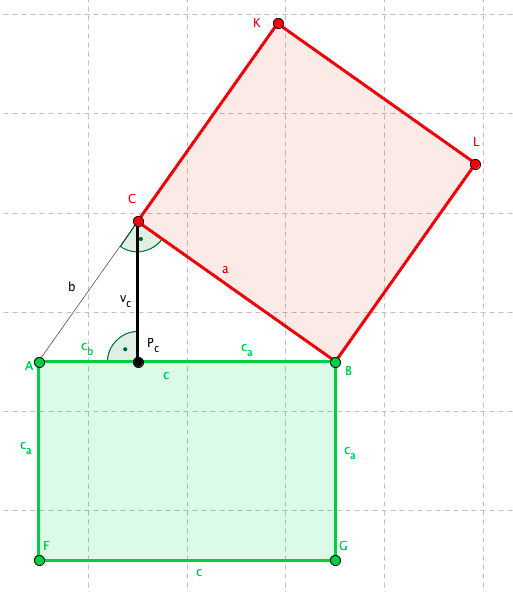
Důkaz můžete opět nalézt na Wikipedii.